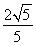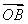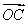题目内容
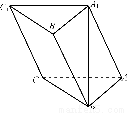
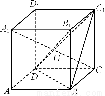
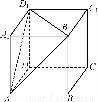
如图所示，直三棱柱ABCA1B1C1中，D、E分别是AB、BB1的中点，AA1＝AC＝CB＝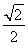
AB.
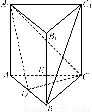
(1)证明：BC1∥平面A1CD；
(2)求二面角DA1CE的正弦值．.
（1）见解析（2）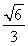
【解析】(1)证明：连结AC1交A1C于点F，则F为AC1中点．又D是AB中点，连结DF，则BC1∥DF.
因为DF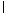
?平面A1CD，BC1
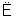平面A1CD，所以BC1∥平面A1CD.
(2)由AC＝CB＝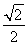
AB得AC⊥BC.以C为坐标原点，
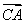的方向为x轴正方向，建立如图所示的空间直角坐标系Cxyz.
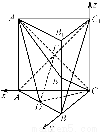
设CA＝2，则D(1，1，0)，E(0，2，1)，A1(2，0，2)，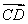
＝(1，1，0)，
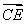＝(0，2，1)，
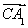＝(2，0，2)．
设n＝(x1，y1，z1)是平面A1CD的法向量，则
即
可取n＝(1，－1，－1)．
同理，设m为平面A1CE的法向量，则
可取m＝(2，1，－2)．
从而cos〈n，m〉＝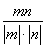
＝
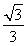，故sin〈n，m〉＝
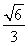.即二面角D-A1C-E的正弦值为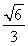
练习册系列答案
小学教材完全解读系列答案
相关题目
