题目内容
(本题满分12分)
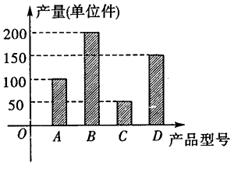
某工厂2010年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加四月份的一个展销会:
(1)问A、B、C、D型号的产品各抽取多少件?
(2)从50件样品随机的抽取2件,求这2件产品恰好是不同型号产品的概率;
 (3)从A、C型号的产品中随机的抽取3件,用
(3)从A、C型号的产品中随机的抽取3件,用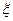 表示抽取A种型号的产品件数,求
表示抽取A种型号的产品件数,求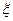 的分布列和数学期望。
的分布列和数学期望。抽取A产品10件,B产品20件,C产品5件,D产品15件,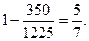
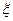 的分布列为
的分布列为
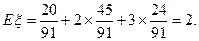
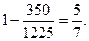
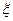 的分布列为
的分布列为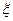 | 0 | 1 | 2 | 3 |
| P |  |  |  | 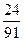 |
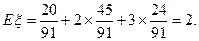
(1)从条表图上可知,共生产产品有50+100+150+200=500(件),
样品比为
所以A、B、C、D四种型号的产品分别取

即样本中应抽取A产品10件,B产品20件,C产品5件,D产品15件。 (3分)
(2)从50件产品中任取2件共有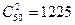 种方法,
种方法,
2件恰为同一产品的方法数为 种,
种,
所以2件恰好为不同型号的产品的概率为
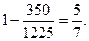 (6分)
(6分)
(3)
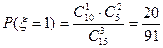

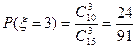 (10分)
(10分)
所以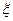 的分布列为
的分布列为
……11分
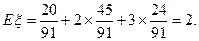 12分
12分
样品比为

所以A、B、C、D四种型号的产品分别取

即样本中应抽取A产品10件,B产品20件,C产品5件,D产品15件。 (3分)
(2)从50件产品中任取2件共有
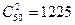 种方法,
种方法,2件恰为同一产品的方法数为
 种,
种,所以2件恰好为不同型号的产品的概率为
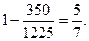 (6分)
(6分)(3)

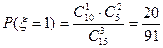

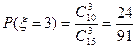 (10分)
(10分)所以
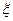 的分布列为
的分布列为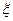 | 0 | 1 | 2 | 3 |
| P |  |  |  | 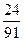 |
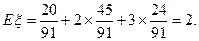 12分
12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
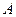 、科目
、科目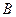 依次进行,只有当科目
依次进行,只有当科目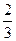 ,每次考科目
,每次考科目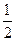 。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试
。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试 的次数为
的次数为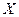 。
。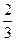 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为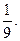
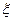 ,求
,求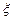 个红球,求随机变量
个红球,求随机变量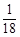
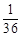
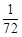
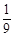
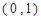 的随机数,则斜边的长小于
的随机数,则斜边的长小于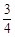 的概率为
的概率为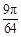
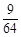
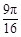
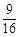

 病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
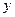

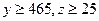 ,求不能通过测试的概率.
,求不能通过测试的概率.