题目内容
某项考试按科目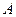
、科目
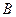依次进行，只有当科目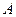成绩合格时，才可以继续参加科目 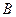的考试。每个科目只允许有一次补考机会，两个科目成绩均合格方可获得该项合格证书，现在某同学将要参加这项考试，已知他每次考科目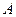成绩合格的概率均为
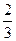，每次考科目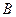成绩合格的概率均为
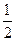。假设他在这项考试中不放弃所有的考试机会，且每次的考试成绩互不影响，记他参加考试
的次数为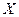
。
(1)求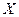的分布列和均值；
(2)求该同学在这项考试中获得合格证书的概率。
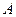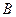、科目依次进行，只有当科目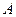成绩合格时，才可以继续参加科目 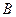的考试。每个科目只允许有一次补考机会，两个科目成绩均合格方可获得该项合格证书，现在某同学将要参加这项考试，已知他每次考科目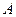成绩合格的概率均为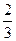，每次考科目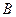成绩合格的概率均为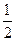。假设他在这项考试中不放弃所有的考试机会，且每次的考试成绩互不影响，记他参加考试的次数为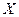。(1)求
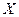的分布列和均值；(2)求该同学在这项考试中获得合格证书的概率。
(1) X的分布列为：
故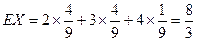
(2) 该同学在这项考试中获得合格证书的概率为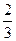
| X | 2 | 3 | 4 |
| P |  | |  |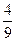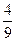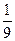
故
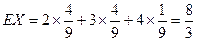
(2) 该同学在这项考试中获得合格证书的概率为
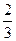
（1
）设该同学“第一次考科目A成绩合格”为事件A1，“科目A补考后成绩合格”为事件A2，“第一次考科目B成绩合格”为事件B1，“科目B补考后成绩合格”为事件B2
由题意知，X可能取得的值为：2，3，4………………………………………………………2分
……………………………………………………
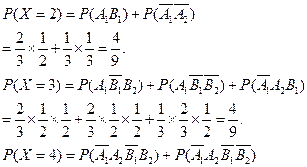
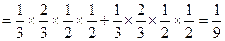……6分
X的分布列为：
故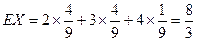 ………………………………………………………8分
（2）设“该同学在这项考试中获得合格证书”为
事件C
则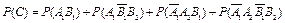
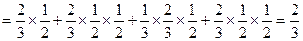
故该同学在这项考试中获得合格证书的概率为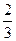 …………………………………………12分
）设该同学“第一次考科目A成绩合格”为事件A1，“科目A补考后成绩合格”为事件A2，“第一次考科目B成绩合格”为事件B1，“科目B补考后成绩合格”为事件B2由题意知，X可能取得的值为：2，3，4………………………………………………………2分
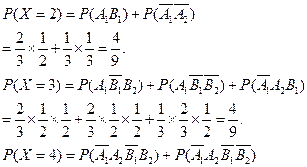
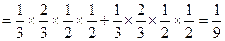…………………………………………………………6分X的分布列为：
| X | 2 | 3 | 4 |
| P | | | |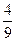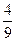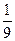
故
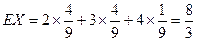………………………………………………………8分（2）设“该同学在这项考试中获得合格证书”为
事件C则
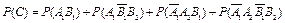
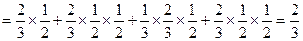
故该同学在这项考试中获得合格证书的概率为
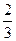…………………………………………12分
练习册系列答案
相关题目
个球,求
．
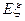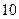里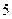
次对走读生的午休情况作了统计，得到
、
、
、
、
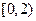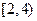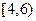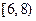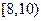，则调查数据表明午休的走读生分布在各个区间内的频率相对稳定，得到了如右图所示的频率分布直方图；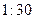
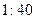
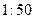
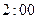
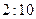
的概率是多少？
，然后上课时间每推迟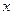
增加2，并以平均每天午休人数作为纵坐标
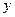，试列出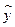
与上课时间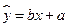
；
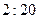时，家距学校的路程在4里路以下的走读生中约有多少人午休？
）
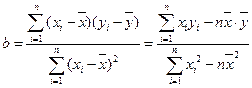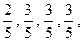且它们相互独立互不影响。
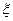表示能成功预约场馆的个数，求随机变量
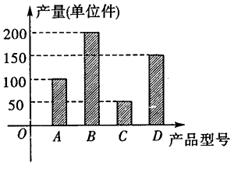（3）从A、C型号的产品中随机的抽取3件，用
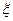表示抽取A种型号的产品件数，求
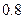,乙射中的概率为
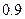.求:(1)两人都射中的概率;(2)两人中恰有一人射中的概率;(3)两人中至少有一人射中的概率;(4)两人中至多有一人射中的概率.
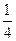，陶艺入选“中国馆·贵宾厅”的概率为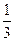
。 
表作中至多有两件作品入选“中国馆·贵宾厅”的概率.
如“0900”，“1909”，“9218”等都为“吉积数”。某地汽车牌照某批次的号码前两位是固定的英文字母，后面是四位数字，则这批号码中末位数字不为4的“吉积数”的概率为（ ）