题目内容
已知圆 ,设点B,C是直线
,设点B,C是直线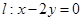 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是 ,点P在线段BC上,过P点作圆M的切线PA,切点为A
,点P在线段BC上,过P点作圆M的切线PA,切点为A
(1)若 ,求直线
,求直线 的方程;
的方程;
(2)经过 三点的圆的圆心是
三点的圆的圆心是 ,求线段
,求线段 (
(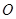 为坐标原点)长的最小值
为坐标原点)长的最小值
(1)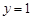 或
或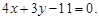 (2)
(2)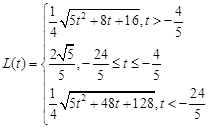
解析试题分析:(1)因为点P在线段BC上,所以可假设点P的坐标 又根据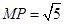 ,所以可求出点P的坐标,同时要检验一下使得点P符合在线段BC上 再通过假设直线的斜率利用点到直线的距离等于圆的半径即可求出直线的斜率,从而得到切线方程
,所以可求出点P的坐标,同时要检验一下使得点P符合在线段BC上 再通过假设直线的斜率利用点到直线的距离等于圆的半径即可求出直线的斜率,从而得到切线方程
(2)因为经过 三点的圆的圆心是
三点的圆的圆心是 ,求线段
,求线段 (
(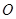 为坐标原点)长 通过假设点P的坐标即可表示线段PM的中点D的坐标(因为
为坐标原点)长 通过假设点P的坐标即可表示线段PM的中点D的坐标(因为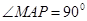 ) 根据两点间的距离公式写出
) 根据两点间的距离公式写出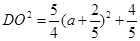 的表达式 接着关键是根据
的表达式 接着关键是根据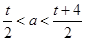 的范围讨论 因为
的范围讨论 因为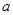 的值受
的值受 的大小决定的 要分三种情况讨论即i)
的大小决定的 要分三种情况讨论即i) 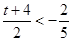 ;ii)
;ii) 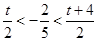 ,iii)
,iii) 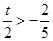 分别求出三种情况的最小值即为所求的结论
分别求出三种情况的最小值即为所求的结论
试题解析:(1)设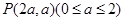 因为
因为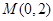 ,
,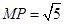 ,所以
,所以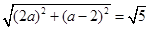 解得
解得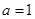 或
或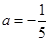 (舍去) 所以
(舍去) 所以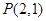 由题意知切线
由题意知切线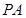 的斜率存在,设斜率为k 所以直线
的斜率存在,设斜率为k 所以直线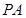 的直线方程为
的直线方程为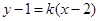 即
即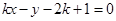
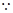 直线PA与圆M相切,
直线PA与圆M相切,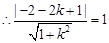 ,解得
,解得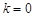 或
或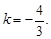
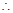 直线PA的方程是
直线PA的方程是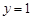 或
或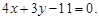 6分
6分
(2)设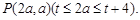
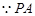 与圆M相切于点A,
与圆M相切于点A,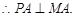
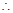 经过
经过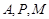 三点的圆的圆心D是线段MP的中点
三点的圆的圆心D是线段MP的中点 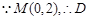 的坐标是
的坐标是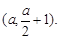
设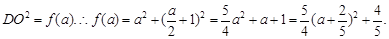
当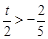 ,即
,即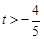 时,
时,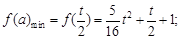
当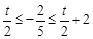 ,即
,即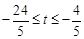 时,
时,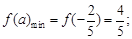
当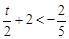 ,即
,即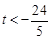 时
时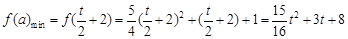
则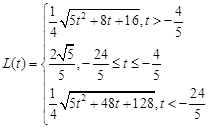
考点:1 直线与圆的位置关系知识 2求圆的切线方程的知识 3 求直角三角形的外接圆的方程的方法 4 解决动区间的二次函数的最值问题的能力 5 分类的思想方法

练习册系列答案
相关题目
 与直线
与直线 相切且与圆
相切且与圆 :
: 外切。
外切。 方程;
方程; 作直线
作直线 交轨迹
交轨迹 两点,
两点, 是
是 点关于坐标原点
点关于坐标原点 的对称点,求证:
的对称点,求证: ;
; :
: 和圆
和圆 :
:

 ,求直线l的方程;
,求直线l的方程; 和
和 ,它们分别与圆
,它们分别与圆 的三个顶点
的三个顶点 ,
,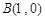 ,
,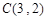 ,其外接圆为
,其外接圆为 .
. 过点
过点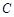 ,且被
,且被 上的任意一点
上的任意一点 ,若在以
,若在以 ,使得点
,使得点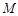 是线段
是线段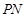 的中点,求
的中点,求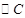 的半径
的半径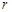 的取值范围.
的取值范围. )两点,且圆心C在直线l:x-y+1=0上,求圆C的标准方程.
)两点,且圆心C在直线l:x-y+1=0上,求圆C的标准方程. 的椭圆T:
的椭圆T: (
( )相切于点M
)相切于点M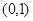 。
。
 、
、 与两曲线分别交于点A、C与点B、D(均不重合)。
与两曲线分别交于点A、C与点B、D(均不重合)。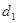 、
、 ,求
,求 的最大值;
的最大值; ,求
,求 轴正半轴上,直线
轴正半轴上,直线 与圆C相切
与圆C相切 的直线
的直线 与圆C交于不同的两点
与圆C交于不同的两点 且为
且为 时,求:
时,求: 的面积.
的面积.