题目内容
3．已知奇函数y=f（x）在定义域R上是单调减函数，且f（a+1）+f（2a）＞0，则a的取值范围是（-∞，-$\frac{1}{3}$）．分析 根据函数奇偶性和单调性之间的关系将不等式进行转化即可．
解答 解：由f（a+1）+f（2a）＞0，得f（2a）＞-f（a+1），
∵奇函数y=f（x）在定义域R上是单调减函数，
∴f（2a）＞-f（a+1）等价为f（2a）＞f（-a-1），
即2a＜-a-1，
即a＜-$\frac{1}{3}$，
故答案为：（-∞，-$\frac{1}{3}$）
点评 本题主要考查不等式的求解，根据函数奇偶性和单调性的性质将不等式进行转化是解决本题的关键．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
13．已知矩形ABCD中，$AB=\sqrt{2}$，BC=1，则$\overrightarrow{AC}•\overrightarrow{DB}$=（ ）
| A． | 1 | B． | -1 | C． | $\sqrt{6}$ | D． | $2\sqrt{2}$ |
11．设复数z=1+i（i是虚数单位），则复数z+$\frac{1}{z}$的虚部是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{2}$i | C． | $\frac{3}{2}$ | D． | $\frac{3}{2}$i |
18．指数函数y=ax，当x＞1（或x＜-1）时，恒有y＞2，则a的取值范围是（ ）
| A． | （$\frac{1}{2}$，1）∪（1，2） | B． | （0，$\frac{1}{2}$）∪（1，2） | C． | （1，2） | D． | （0，$\frac{1}{2}$）∪（2，+∞） |
8．在等比数列{an}中，a1=8，a4=1，则a7=（ ）
| A． | $\frac{1}{16}$ | B． | $\frac{1}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
15．已知定义域为R的奇函数f（x）的导函数为f′（x），当x≠0时，f'（x）+$\frac{f（x）}{x}$＞0，若a=$\frac{1}{2}f（\frac{1}{2}）\;\;b=-2f（-2）\;\;c=ln2•f（ln2）$，则下列关于a，b，c的大小关系正确的是（ ）
| A． | a＞b＞c | B． | a＞c＞b | C． | c＞b＞a | D． | b＞c＞a |
12．如图，给出事件A与B的关系示意图，则（ ）
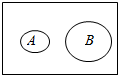
| A． | A⊆B | B． | A与B互斥 | ||
| C． | B⊆A | D． | A与B互为对立事件 |