题目内容
【题目】已知函数![]() 在定义域内有两个不同的极值点.
在定义域内有两个不同的极值点.
(Ⅰ)求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() 有两个不同的极值点
有两个不同的极值点![]() ,且
,且![]() ,若不等式
,若不等式![]() 恒成立,求正实数
恒成立,求正实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)求导得![]() ,再转化为
,再转化为![]() 与
与![]() 的图像在
的图像在![]() 上有两个不同的交点,再分析
上有两个不同的交点,再分析![]() 的函数单调性与最值,进而数形结合求解即可.
的函数单调性与最值,进而数形结合求解即可.
(Ⅱ)设![]() 是
是![]() 的两个根,代入相减可得
的两个根,代入相减可得![]() ,再对
,再对![]() 两边取对数,化简即证
两边取对数,化简即证 ,再构造
,再构造![]() ,分析函数的单调性证明最值,从而求得取值范围即可.
,分析函数的单调性证明最值,从而求得取值范围即可.
(Ⅰ)由题意, ![]() 有两个不同的根,
有两个不同的根,
故方程![]() 在
在![]() 上有两个不同的根,转化为函数
上有两个不同的根,转化为函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点.
上有两个不同交点.
![]() ,故
,故![]() 时,
时,![]() .
. ![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
所以![]()
又![]() ,故
,故![]() 时,
时, ![]() ,
,![]() 时,
时, ![]()
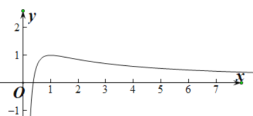
由图象可得:![]()
(Ⅱ)由(Ⅰ)知:设![]() 是
是![]() 的两个根,
的两个根,
故![]() ,
,![]() ,相减可得
,相减可得![]() .
.
故![]()
![]() ,又
,又![]() ,故上式即为
,故上式即为
令![]() ,则
,则![]() 对
对![]() 恒成立.
恒成立.
设![]() ,则
,则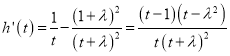 ,
,![]()
①若![]() ,当
,当![]() 时,
时, ![]() ,
,![]() 时,
时, ![]()
故![]() 在
在![]() 上单调递减,故当
上单调递减,故当![]() 时
时![]() ,不合题意;
,不合题意;
②若![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上单调递增.
上单调递增.
故![]() 时,
时, ![]() ,即
,即![]() 恒成立.
恒成立.
综上:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某人沿固定路线开车上班,沿途共有![]() 个红绿灯,他对过去
个红绿灯,他对过去![]() 个工作日上班途中的路况进行了统计,得到了如表的数据:
个工作日上班途中的路况进行了统计,得到了如表的数据:
上班路上遇见的红灯数 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
若一路绿灯,则他从家到达公司只需用时![]() 分钟,每遇一个红灯,则会多耗时
分钟,每遇一个红灯,则会多耗时![]() 分钟,以频率作为概率的估计值
分钟,以频率作为概率的估计值
(1)试估计他平均每天上班需要用时多少分钟?
(2)若想以不少于![]() 的概率在早上
的概率在早上![]() 点前(含
点前(含![]() 点)到达公司,他最晚何时要离家去公司?
点)到达公司,他最晚何时要离家去公司?
(3)公司规定,员工应早上![]() 点(含
点(含![]() 点)前打卡考勤,否则视为迟到,每迟到一次,会被罚款
点)前打卡考勤,否则视为迟到,每迟到一次,会被罚款![]() 元.因某些客观原因,在接下来的
元.因某些客观原因,在接下来的![]() 个工作日里,他每天早上只能
个工作日里,他每天早上只能![]() 从家出发去公司,求他因迟到而被罚款的期望.
从家出发去公司,求他因迟到而被罚款的期望.