题目内容
【题目】已知椭圆 ![]() 的一个焦点与抛物线
的一个焦点与抛物线 ![]() 的焦点
的焦点 ![]() 重合,且点
重合,且点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() ,
, ![]() 与
与 ![]() 的公共弦长为
的公共弦长为 ![]() .
.
(1)求椭圆 ![]() 的方程及点
的方程及点 ![]() 的坐标;
的坐标;
(2)过点 ![]() 的直线
的直线 ![]() 与
与 ![]() 交于
交于 ![]() 两点,与
两点,与 ![]() 交于
交于 ![]() 两点,求
两点,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:∵ ![]() 的焦点
的焦点 ![]() 的坐标为
的坐标为 ![]() ,
,
由点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() 得
得 ![]() .
.
∵ ![]() ,解得
,解得 ![]() ,又
,又 ![]() 为椭圆的一个焦点,∴
为椭圆的一个焦点,∴ ![]() .
.
∵ ![]() 与
与 ![]() 的公共弦长为
的公共弦长为 ![]() ,
, ![]() 与
与 ![]() 都关于
都关于 ![]() 轴对称,
轴对称,
而 ![]() 的方程为
的方程为 ![]() ,从而
,从而 ![]() 与
与 ![]() 的公共点的坐标为
的公共点的坐标为 ![]() ,
,
∴ ![]() ②,
②,
联立①②解得 ![]() ,
,
∴ ![]() 的方程为
的方程为 ![]() ,点
,点 ![]() 的坐标为
的坐标为 ![]()
(2)解:当 ![]() 过点
过点 ![]() 且垂直于
且垂直于 ![]() 轴时,
轴时, ![]() 的方程为
的方程为 ![]() 代入
代入 ![]() 求得
求得 ![]() ,
,
∴ ![]() ,把
,把 ![]() 代入
代入 ![]() 求得
求得 ![]() ,∴
,∴ ![]() ,
,
此时 ![]() .
.
当 ![]() 与
与 ![]() 轴不垂直时,要使
轴不垂直时,要使 ![]() 与
与 ![]() 有两个交点,可设
有两个交点,可设 ![]() 的方程为
的方程为 ![]() ,
,
此时设 ![]()
把直线 ![]() 的方程与椭圆
的方程与椭圆 ![]() 的方程联立得
的方程联立得 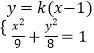 ,
,
消去 ![]() 化简得
化简得 ![]() ,
,
可得 ![]() ,
,
∴ ![]() ,
,
把直线 ![]() 的方程与抛物线
的方程与抛物线 ![]() 的方程联立得
的方程联立得 ![]() ,
,
消去 ![]() 化简得
化简得 ![]() ,
,
可得 ![]() ,
,
∴ ![]() ,
,
![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,
,
综上可得 ![]() 的取值范围是
的取值范围是 ![]()
【解析】(1)由已知求出抛物线的焦点可得出 ![]() ,再利用点到直线的距离公式
,再利用点到直线的距离公式![]() 求得c的值,进而得到焦点的坐标然后求出抛物线的方程,再由已知再设出公共端点的坐标利用弦长公式 代入数值求出交点坐标,然后把数值带入到椭圆的方程计算得出a、b的值进而得到椭圆的方程。(2)由题意结合直线点斜式设出直线的方程,代入到抛物线的方程和椭圆的方程消去y得到的关于x的一元二次方程,利用韦达定理
求得c的值,进而得到焦点的坐标然后求出抛物线的方程,再由已知再设出公共端点的坐标利用弦长公式 代入数值求出交点坐标,然后把数值带入到椭圆的方程计算得出a、b的值进而得到椭圆的方程。(2)由题意结合直线点斜式设出直线的方程,代入到抛物线的方程和椭圆的方程消去y得到的关于x的一元二次方程,利用韦达定理![]() 和弦长公式
和弦长公式![]() 即可求得
即可求得![]() 的代数式,把结果代入到要求的式子里结合该式子的特点整理即可求出上式的取值范围。
的代数式,把结果代入到要求的式子里结合该式子的特点整理即可求出上式的取值范围。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目