题目内容
【题目】已知![]() .
.
(1)试求![]() 在
在![]() 上的最大值;
上的最大值;
(2)已知![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行,若存在
轴平行,若存在![]() ,
,![]() ,使得
,使得![]() ,证明:
,证明:![]() .
.
【答案】(1)当![]() 时
时![]() ;当
;当![]() 时
时![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)先求导数![]() ,然后对
,然后对![]() 分类讨论,判断单调性,求解即可.
分类讨论,判断单调性,求解即可.
(2)由题意可知,![]() ,则
,则![]() ,从而确定
,从而确定![]() 单调性,再根据
单调性,再根据![]() 的正负,确定其函数的大致图像,从而确定有
的正负,确定其函数的大致图像,从而确定有![]() ,要证
,要证![]() ,只需证
,只需证![]() ,只需证明
,只需证明![]() ,只需证
,只需证![]() ,构造函数
,构造函数![]() ,利用导数研究函数的单调性,证明不等式,即可.
,利用导数研究函数的单调性,证明不等式,即可.
(1)![]() ,
,
当![]() 时,则
时,则![]() 对任意
对任意![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
所以![]() 在
在![]() 单调递增.
单调递增.
则![]() 的最大值为
的最大值为![]() ;
;
当![]() 时,令
时,令![]() ,即
,即![]()
当![]() ,即
,即![]() 时,
时,
当![]() 时
时![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时
时![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,![]() .
.
当![]() 即
即![]() 时,
时,![]() 对任意
对任意![]() 恒成立,
恒成立,
即![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 单调递增.
单调递增.
则![]() 的最大值为
的最大值为![]() ;
;
综上所述:当![]() 时
时![]() ;
;
当![]() 时
时![]() .
.
(2)因为![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行,
轴平行,
所以![]() ,则
,则![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减.
上单调递减.
又因为![]() 时有
时有![]() ;
;![]() 时有
时有![]() ,
,
根据图象可知,若![]() ,则有
,则有![]() ;
;
要证![]() ,只需证
,只需证![]() ;
;
又因为![]() ,所以
,所以![]() ;
;
因为![]() 在
在![]() 上单调递减,从而只需证明
上单调递减,从而只需证明![]() ,
,
只需证![]()
只需证![]()
设![]() ,则
,则![]() .
.
由![]() 的单调性可知,
的单调性可知,![]() .
.
则![]() ,即
,即![]() .
.
所以![]() ,即
,即![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() .
.
从而不等式![]() 得证.
得证.
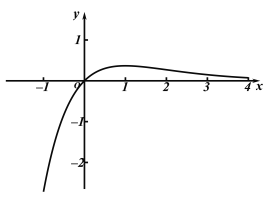

【题目】函数f(x)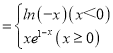 ,若关于x的方程f2(x)﹣af(x)+a﹣a2=0有四个不等的实数根,则a的取值范围是( )
,若关于x的方程f2(x)﹣af(x)+a﹣a2=0有四个不等的实数根,则a的取值范围是( )
A.![]() B.(﹣∞,﹣1)∪[1,+∞)
B.(﹣∞,﹣1)∪[1,+∞)
C.(﹣∞,﹣1)∪{1}D.(﹣1,0)∪{1}
【题目】在国家“大众创业,万众创新”战略下,某企业决定加大对某种产品的研发投入.为了对新研发的产品进行合理定价,将该产品按事先拟定的价格试销,得到一组检测数据如表所示:
试销价格 |
|
|
|
|
|
|
产品销量 |
|
|
|
|
|
|
已知变量![]() 且有线性负相关关系,现有甲、乙、丙三位同学通过计算求得回归直线方程分别为:甲
且有线性负相关关系,现有甲、乙、丙三位同学通过计算求得回归直线方程分别为:甲![]() ;丙
;丙![]() ,其中有且仅有一位同学的计算结果是正确的.
,其中有且仅有一位同学的计算结果是正确的.
(1)试判断谁的计算结果正确?
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过![]() ,则称该检测数据是“理想数据”,现从检测数据中随机抽取
,则称该检测数据是“理想数据”,现从检测数据中随机抽取![]() 个,求“理想数据”的个数
个,求“理想数据”的个数![]() 的分布列和数学期望.
的分布列和数学期望.