题目内容
15.已知函数f(x)=alnx-ax-3(a<0).(1)求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[0,1],函数g(x)=x3+x2[f′(x)+m]在区间(t,2)上总不是单调函数,其中f′(x)为f(x)的导函数,求实数m的取值范围.
分析 (1)求导,利用导数的正负确定函数的单调区间;
(2)求导,利用零点存在定理判定g′(x)在(t,2)上总存在零点计算即得结论.
解答 解:(1)根据题意知,f′(x)=$\frac{a(1-x)}{x}$(x>0),
令f′(x)=0得:x=1,
∴当a<0时,f(x)的单调递增区间为(1,+∞)、f(x)的单调递减区间为(0,1];
(2)∵函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,
∴f′(2)=-$\frac{a}{2}$=1,即a=-2,
∴f(x)=-2lnx+2x-3,
∴g(x)=x3+(m+2)x2-2xm,
∴g′(x)=3x2+(2m+4)x-2,
∵g(x)在区间(t,2)上总不是单调函数,且g′(0)=-2,
∴$\left\{\begin{array}{l}{g′(t)<0}\\{g′(2)>0}\end{array}\right.$,
由题意知:对于任意的t∈[0,1],g′(t)<0恒成立,
∴$\left\{\begin{array}{l}{g′(0)<0}\\{g′(1)<0}\\{g′(2)>0}\end{array}\right.$,
∴-$\frac{9}{2}$<m<-$\frac{5}{2}$.
点评 利用导数研究函数的单调性、极值、最值及与函数有关的综合题,都体现了导数的重要性;此类问题往往从求导入手,思路清晰;但综合性较强,需学生有较高的逻辑思维和运算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
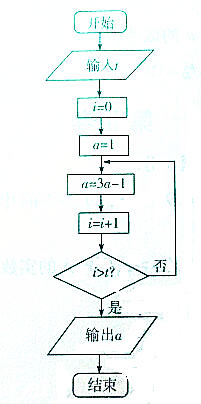 如图是一个程序框图,若输出a的值为365,则输入的t的值可以为5.
如图是一个程序框图,若输出a的值为365,则输入的t的值可以为5.