题目内容
【题目】如图,已知三棱柱ABC-A1B1C1,侧面ABB1A1为菱形,侧面ACC1A1为正方形,侧面ABB1A1⊥侧面ACC1A1.
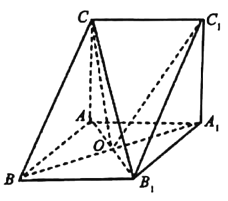
(1)求证:A1B⊥平面AB1C;
(2)若AB=2,∠ABB1=60°,求三棱锥C1-COB1的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)先根据面面垂直的性质定理得到![]() 平面
平面![]() ,由此得到
,由此得到![]() ,结合菱形的几何性质得到
,结合菱形的几何性质得到![]() ,进而证得
,进而证得![]() 平面
平面![]() .(2)先证得
.(2)先证得![]() 平面
平面![]() ,由此将所求几何体的体积,转化为三棱锥
,由此将所求几何体的体积,转化为三棱锥![]() 的体积.由(1)得
的体积.由(1)得![]() 为三棱锥
为三棱锥![]() 的高,根据三棱锥的体积公式计算出所求几何体的体积.
的高,根据三棱锥的体积公式计算出所求几何体的体积.
解:(1)因为侧面![]()
![]() 侧面
侧面![]() ,侧面
,侧面![]() 为正方形,所以
为正方形,所以![]() 平面
平面![]() ,
,![]() , 又侧面
, 又侧面![]() 为菱形,所以
为菱形,所以![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)因为![]() ,所以,
,所以,![]() 平面
平面![]() ,所以,三棱锥
,所以,三棱锥![]() 的体积等于三棱锥
的体积等于三棱锥![]() 的体积;
的体积; ![]() 平面
平面![]() ,所以
,所以![]() 为三棱锥
为三棱锥![]() 的高,
的高,
因为![]() ,
,![]() ,
,
所以![]()

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目


