题目内容
【题目】我国南北朝时期的数学家张丘建是世界数学史上解决不定方程的第一人，他在《张丘建算经》中给出一个解不定方程的百鸡问题，问题如下：鸡翁一，值钱五，鸡母一，值钱三，鸡雏三，值钱一．百钱买百鸡，问鸡翁母雏各几何？用代数方法表述为：设鸡翁、鸡母、鸡雏的数量分别为
，
，
，则鸡翁、鸡母、鸡雏的数量即为方程组
的解．其解题过程可用框图表示如下图所示，则框图中正整数
的值为 ______．
【答案】4
【解析】分析：由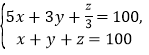
得y=25﹣
x，结合x=4t，可得框图中正整数m的值．
详解：由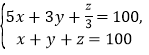得：y=25﹣x，故x必为4的倍数，
当x=4t时，y=25﹣7t，
由y=25﹣7t＞0得：t的最大值为3，
故判断框应填入的是t＜4？，
即m=4，
故答案为：4
点睛: 本题考查的知识点是程序框图，根据已知分析出y与t的关系式及t的取值范围，是解答的关键．
练习册系列答案
相关题目
【题目】某研究机构对高三学生的记忆力
和判断力
进行统计分析，得下表数据：
| 6 | 8 | 10 | 12 |
| 2 | 3 | 5 | 6 |
（1）请在图中画出上表数据的散点图；
（2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（3）试根据（2）求出的线性回归方程，预测记忆力为9的同学的判断力．
相关公式：
，
.
