题目内容
16.已知(x2+$\frac{2}{\sqrt{x}}$)n的展开式的二项式系数之和为32,则其展开式中常数项为80.分析 由二项式系数的性质求得n,写出二项展开式的通项,由x的指数为0求得r,则展开式中常数项可求.
解答 解:由题意知,2n=32,即n=5.
∴(x2+$\frac{2}{\sqrt{x}}$)n=(x2+$\frac{2}{\sqrt{x}}$)5,
由${T}_{r+1}={C}_{5}^{r}({x}^{2})^{5-r}(\frac{2}{\sqrt{x}})^{r}$=${2}^{r}{C}_{5}^{r}{x}^{10-\frac{5r}{2}}$.
令10-$\frac{5r}{2}=0$,得r=4.
∴展开式中常数项为${T}_{5}={2}^{4}×{C}_{5}^{4}=80$.
故答案为:80.
点评 本题考查了二项式系数的性质,关键是熟记二项展开式的通项,是基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
16.已知全集U={1,2,3,4,5,6},集合A={2,3,5},集合B={1,3,4,6},则集合A∩∁UB=( )
| A. | {3} | B. | {2,5} | C. | {1,4,6} | D. | {2,3,5} |
11.抛物线y2=4x,直线l经过该抛物线的焦点F与抛物线交于A、B两点(A点在第一象限),且$\overrightarrow{BA}$=4$\overrightarrow{BF}$,则三角形AOB(O为坐标原点)的面积为( )
| A. | $\frac{8\sqrt{3}}{3}$ | B. | $\frac{8\sqrt{2}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
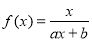 (
(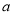 ,
,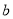 为常数,
为常数, )满足
)满足 ,且
,且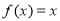 有唯一解.
有唯一解.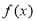 的解析式;
的解析式; ,且
,且 (
( ,
, ),求证:数列
),求证:数列 为等差数列.
为等差数列.