题目内容
已知函数f(x)=2
sinωxcosωx+2cos2ωx-1(ω>0)的图象上的一个最低点为P,离P最近的两个最高点分别为M、N,且
•
=16-
.
(1)求ω的值;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,若f(
)=1,且a=2,b+c=4,求△ABC的面积.
| 3 |
| PM |
| PN |
| π2 |
| 16 |
(1)求ω的值;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,若f(
| A |
| 2 |
(1)f(x)=
sin2ωx+cos2ωx=2sin(2ωx+
),
令P(x0,-2),M(x0-
,2),N(x0+
,2),
∴
•
=-
+16=16-
,
∴T=
=
,
则ω=2;
(2)∵f(
)=2sin(2A+
)=1,
∴2A+
=
,即A=
,
又a2=b2+c2-2bccosA,
∴4=b2+c2-bc=(b+c)2-3bc,
∵b+c=4,
∴bc=4,
则S△ABC=
bcsinA=
.
| 3 |
| π |
| 6 |
令P(x0,-2),M(x0-
| T |
| 2 |
| T |
| 2 |
∴
| PM |
| PN |
| T2 |
| 4 |
| π2 |
| 16 |
∴T=
| π |
| 2 |
| 2π |
| 2ω |
则ω=2;
(2)∵f(
| A |
| 2 |
| π |
| 6 |
∴2A+
| π |
| 6 |
| 5π |
| 6 |
| π |
| 3 |
又a2=b2+c2-2bccosA,
∴4=b2+c2-bc=(b+c)2-3bc,
∵b+c=4,
∴bc=4,
则S△ABC=
| 1 |
| 2 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
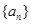 为等差数列,且
为等差数列,且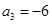 ,
,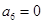 .
.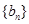 满足
满足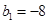 ,
,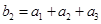 ,求
,求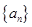 的首项
的首项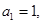 公差
公差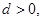 且
且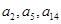 分别是等比数列
分别是等比数列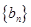 的
的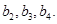
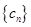 对任意正整数
对任意正整数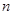 均有
均有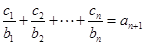 成立,求
成立,求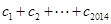 的值.
的值.