题目内容
已知数列{an}各项均为正数,其前n项和为Sn,且满足4Sn=(an+1)2.
(1)求{an}的通项公式;(2)设bn=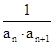 ,数列{bn}的前n项和为Tn,求Tn的最小值.
,数列{bn}的前n项和为Tn,求Tn的最小值.
(1)求{an}的通项公式;(2)设bn=
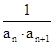 ,数列{bn}的前n项和为Tn,求Tn的最小值.
,数列{bn}的前n项和为Tn,求Tn的最小值.(1)an=2n-1;(2) .
.
 .
.试题分析:(1)本小题可化归为an+1=Sn+1-Sn,整理为4an+1=an+12-an2+2an+1-2an再因式分解为2(an+1+an)=(an+1+an)(an+1-an),即可得到an+1-an=2,根据等差数列的定义,可知{an}为等差数列,易得其通项公式;(2)本小题bn通项公式先进行裂项,利用裂项相消法可求得Tn的值,可证明Tn+1>Tn,易知{Tn}为递增数列,则最小值为T1.
试题解析:(1)因为(an+1)2=4Sn,所以Sn=
 ,Sn+1=
,Sn+1= .
.所以Sn+1-Sn=an+1=
 即4an+1=an+12-an2+2an+1-2an, ∴2(an+1+an)=(an+1+an)(an+1-an).
即4an+1=an+12-an2+2an+1-2an, ∴2(an+1+an)=(an+1+an)(an+1-an). 因为an+1+an≠0,所以an+1-an=2,即{an}为公差等于2的等差数列.由(a1+1)2=4a1,解得a1=1,所以an=2n-1.
(2)由(1)知bn=
 =
= ,∴Tn=b1+b2+…+bn=
,∴Tn=b1+b2+…+bn=

∵Tn+1-Tn=
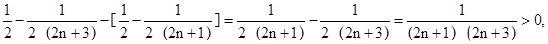
∴Tn+1>Tn,∴数列{Tn}为递增数列,∴Tn的最小值为T1=
 .
.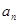 与
与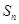 的关系:
的关系: ,等差数列的定义,裂项相消法,递增数列的定义.
,等差数列的定义,裂项相消法,递增数列的定义.
练习册系列答案
相关题目
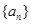 为等差数列,且
为等差数列,且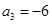 ,
,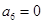 .
.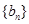 满足
满足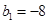 ,
,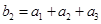 ,求
,求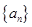 的首项
的首项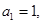 公差
公差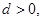 且
且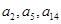 分别是等比数列
分别是等比数列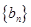 的
的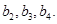
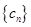 对任意正整数
对任意正整数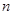 均有
均有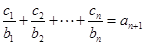 成立,求
成立,求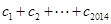 的值.
的值.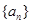 的前
的前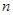 项和为
项和为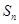 ,
,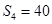 ,
,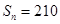 ,
,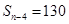 ,则
,则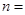 ( )
( )



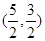 有n条弦的长度成等差数列,最小弦长为数列的首项a1,最大弦长为an,若公差
有n条弦的长度成等差数列,最小弦长为数列的首项a1,最大弦长为an,若公差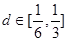 ,那么n的可能取值为____ .
,那么n的可能取值为____ . 中,前
中,前 项和
项和 ,若
,若 ,
, ,则
,则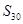 = .
= .