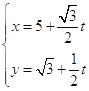题目内容
【题目】在直角坐标系 ![]() 中,以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系.已知曲线
中,以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系.已知曲线 ![]() (t为参数),曲线
(t为参数),曲线 ![]() ;
;
(1)将曲线 ![]() 化成普通方程,将曲线
化成普通方程,将曲线 ![]() 化成参数方程;
化成参数方程;
(2)判断曲线 ![]() 和曲线
和曲线 ![]() 的位置关系.
的位置关系.
【答案】
(1)解:∵ ,∴ ,
代入 得, ,即 .
∴曲线 的普通方程是 .
将 代入曲线 的方程 ,得
即 .
设 ,
得曲线 的参数方程: ![]() ( 为参数)
( 为参数)
(2)解:由(1)知,曲线 是经过点 的直线,曲线 是以 为圆心半径为 的圆.
∵ ,
∴ 在曲线 内,
∴曲线 和曲线 相交.
【解析】分析:本题主要考查了参数方程化成普通方程,解决问题的关键是(1)利用极坐标与普通坐标之间的转化即可求出曲线 ![]() 的普通方程,从而可得到曲线
的普通方程,从而可得到曲线 ![]() 的参数方程,利用消去参数的方程即可求出直线的普通方程;(2)求出曲线曲线
的参数方程,利用消去参数的方程即可求出直线的普通方程;(2)求出曲线曲线 ![]() 的圆心到直线的距离并与半径作比较,即可得到直线与曲线
的圆心到直线的距离并与半径作比较,即可得到直线与曲线 ![]() 的位置关系.
的位置关系.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).


(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式:  ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |