题目内容
【题目】已知椭圆
的长轴长为
，焦距为2，抛物线
的准线经过C的左焦点F.
（1）求C与M的方程；
（2）直线l经过C的上顶点且l与M交于P，Q两点，直线FP，FQ与M分别交于点D（异于点P），E（异于点Q），证明:直线DE的斜率为定值.
【答案】（1）C：
，M：
（2）证明见解析
【解析】
（1）由题意可得
，
的值，运用
，求得
，可得椭圆
的方程，由
的准线经过点
，求得
，即可得解的方程；
（2）设直线
的方程为
，联立直线与抛物线的方程，设
，
，运用韦达定理得
之间的关系，再联立直线
与抛物线的方程解得
的坐标，同理可得出
的坐标，代入两点间斜率计算公式即可得结果.
（1）由题意，得
，
，所以
，
，
所以
，所以C的方程为，
所以
，由于M的准线经过点F，
所以
，所以
，故M的方程为.
（2）证明:由题意知，l的斜率存在，故设直线l的方程为，
由
，得
.
设，，
则
，即
且
，
，
.
又直线FP的方程为
，
由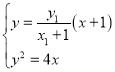
，得
，
所以
，所以
，从而D的坐标为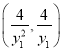
.
同理可得E的坐标为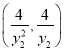
，
所以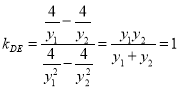
为定值.
【题目】某学校有30位高级教师，其中60%人爱好体育锻炼，经体检调查，得到如下列联表.
身体好 | 身体一般 | 总计 | |
爱好体育锻炼 | 2 | ||
不爱好体育锻炼 | 4 | ||
总计 | 20 |
（1）根据以上信息完成
列联表，并判断有多大把握认为“身体好与爱好体育锻炼有关系”？
（2）现从身体一般的教师中抽取3人，记3人中爱好体育锻炼的人数为
，求的分布列及数学期望.
参考公式：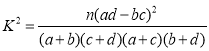
，其中
.
临界值表：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】近年来，我国电子商务蓬勃发展.2016年“618”期间，某网购平台的销售业绩高达516亿元人民币，与此同时，相关管理部门推出了针对该网购平台的商品和服务的评价系统.从该评价系统中选出200次成功交易，并对其评价进行统计，网购者对商品的满意率为0.6，对服务的满意率为0.75，其中对商品和服务都满意的交易为80次.
（1）根据已知条件完成下面的
列联表，并回答能否有
的把握认为“网购者对商品满意与对服务满意之间有关系”?
对服务满意 | 对服务不满意 | 合计 | |
对商品满意 | 80 | ||
对商品不满意 | 10 | ||
合计 | 200 |
（2）若将频率视为概率，某人在该网购平台上进行的3次购物中，设对商品和服务都满意的次数为随机变量
，求的分布列和数学期望
.
临界值表：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
的观测值：
（其中
）.
