Question

【题目】某中学将100名高一新生分成水平相同的甲，乙两个“平行班”，每班50人.陈老师采用A,B两种不同的教学方式分别在甲，乙两个班级进行教改实验.为了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下，计成绩不低于90分者为“成绩优秀”.

（1）从乙班样本的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；

（2）由以上统计数据填写下面2x2列联表，并判断是否有的把握认为“成绩优秀”与教学方式有关.

	甲班（A方式）	乙班（B方式）	总计
成绩优秀
成绩不优秀
总计

附：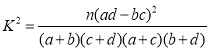

/tr>

P（	0.25	0.15	0.10	0.05	0.025
k	1.323	2.072	2.706	3.841	5.024

Answer 1

【答案】（1）；（2）有的把握认为“成绩优秀”与教学方式有关.

【解析】

试题（1）设“抽出的两个均“成绩优秀”“为事件A. 从不低于86分的成绩中随机抽取2个的基本事件为（86,93），（86,96），（86,97），（86,99）（86,99），（93,96），（93,97），（93,99），（93,99），（96,97），（96,99），（96,99），（97,99），（97,99），（99,99），共15个，而事件A包含基本事件：（93,96），（93,97），（93,99），（93,99），（96,97），（96,99），（96,99），（97,99），（97,99），（99,99），共10个，从而可得所求概率为P（A）=；

（2）由已知数据得：

	甲班（A方式）	乙班（B方式）	总计
成绩优秀	1	5	6
成绩不优秀	19	15	34
总计	20	20	40

根据2x2列联表中数据，，由于，所以有的把握认为“成绩优秀”与教学方式有关.

试题解析：（1）设“抽出的两个均“成绩优秀”“为事件A. 从不低于86分的成绩中随机抽取2个的基本事件为（86,93），（86,96），（86,97），（86,99）（86,99），（93,96），（93,97），（93,99），（93,99），（96,97），（96,99），（96,99），（97,99），（97,99），（99,99），共15个，

而事件A包含基本事件：（93,96），（93,97），（93,99），（93,99），（96,97），（96,99），（96,99），（97,99），（97,99），（99,99），共10个.

所以所求概率为P（A）=

（2）由已知数据得：

	甲班（A方式）	乙班（B方式）	总计
成绩优秀	1	5	6
成绩不优秀	19	15	34
总计	20	20	40

根据2x2列联表中数据，，由于，

所以有的把握认为“成绩优秀”与教学方式有关.