题目内容
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,其中
,其中![]() 是数列
是数列![]() 的前n项和.
的前n项和.
(1)求![]() 和
和![]() 的值及数列
的值及数列![]() 的通项公式;
的通项公式;
(2)设![]() .
.
①若![]() ,求k的值;
,求k的值;
②求证:数列(![]() 中的任意一项总可以表示成该数列其他两项之积.
中的任意一项总可以表示成该数列其他两项之积.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)①1,②见解析
;(2)①1,②见解析
【解析】
(1)利用递推关系式求出数列的前几项,同时求出数列![]() 的通项公式;(2)结合第一问的结论求出
的通项公式;(2)结合第一问的结论求出![]() ,①直接代入
,①直接代入![]() 即可求解;②对于给定的
即可求解;②对于给定的![]() ,若存在
,若存在![]() ,
,![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,只要找到相应的整数,即可证明.
,只要找到相应的整数,即可证明.
(1)![]() 时,
时,![]() ,所以
,所以![]() ,
,
![]() 时,
时,![]() ,所以
,所以![]() ,所以
,所以![]() .
.
由![]() ,①
,①
所以![]() ,②
,②
由②![]() ①得
①得![]() ,
,
即![]() ,③
,③
当![]() 时,
时,![]() ,④
,④
由③![]() ④得
④得![]() ,
,
即![]() ,
,
所以数列![]() 是首项为0,公差为2的等差数列,
是首项为0,公差为2的等差数列,
故数列![]() 的通项公式是
的通项公式是![]() .
.
(2)![]() ;
;
![]()
![]() ;
;
①![]() ;
;
![]()
![]() .
.
②对于给定的![]() ,若存在
,若存在![]() ,
,![]() ,
,![]() ,
,![]() ,使得
,使得![]() ;
;
![]() ,只需
,只需![]() ,
,
两边取倒数,即![]() ,即
,即![]() ;
;
即![]() ,
,![]() ;取
;取![]() ,则
,则![]() ;
;
![]() ;
;
![]() 对数列
对数列![]() 中的任意一项,总可以表示成该数列其他两项之积.
中的任意一项,总可以表示成该数列其他两项之积.

【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该公司将最近承揽的
元.该公司将最近承揽的![]() 件包裹的重量统计如下:
件包裹的重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近![]() 天,每天揽件数量统计如下表:
天,每天揽件数量统计如下表:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来![]() 天内恰有
天内恰有![]() 天揽件数在
天揽件数在![]() 之间的概率;
之间的概率;
(2)(i)估计该公司对每件包裹收取的快递费的平均值;
(ii)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,工资
件,工资![]() 元.公司正在考虑是否将前台工作人员裁减
元.公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
【题目】随着科技的发展,网购已经逐渐融入了人们的生活.在家里面不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,如果近的话当天买当天就能送到,或者第二天就能送到,所以网购是非常方便的购物方式.某公司组织统计了近五年来该公司网购的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年)的数据,列表如下:
(单位:年)的数据,列表如下:
| 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
(1)依据表中给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).(若
并加以说明(计算结果精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式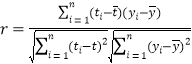
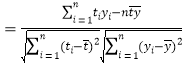 ,参考数据
,参考数据![]() .
.
(2)建立![]() 关于
关于![]() 的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
(参考公式: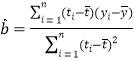
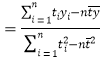 ,
,![]() )
)
【题目】某中学将100名高一新生分成水平相同的甲,乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲,乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下,计成绩不低于90分者为“成绩优秀”.

(1)从乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的两个均“成绩优秀”的概率;
(2)由以上统计数据填写下面2x2列联表,并判断是否有![]() 的把握认为“成绩优秀”与教学方式有关.
的把握认为“成绩优秀”与教学方式有关.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附: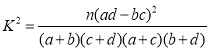
P( | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | /tr>