题目内容
2.(1)求过x+y+1=0与2x+3y+6=0的交点,且与2x-y+5=0垂直的直线的方程;(2)求经过点A(0,0)和B(1,1),且圆心在x轴上的圆的方程.
分析 (1)解方程组$\left\{\begin{array}{l}{x+y+1=0}\\{2x+3y+6=0}\end{array}\right.$,求出x+y+1=0与2x+3y+6=0的交点,再求出与2x-y+5=0垂直的直线的斜率,由此利用点斜式方程能求出所求的直线方程.
(2)设圆心(a,0),则$\sqrt{{a}^{2}}=\sqrt{(a-1)^{2}+(0-1)^{2}}$,由此能求出所求的圆的方程.
解答 解:(1)解方程组$\left\{\begin{array}{l}{x+y+1=0}\\{2x+3y+6=0}\end{array}\right.$,得x+y+1=0与2x+3y+6=0的交点为(3,-4),
∵2x-y+5=0的斜率k=2,∴与2x-y+5=0垂直的直线的斜率${k}^{'}=-\frac{1}{k}=-\frac{1}{2}$,
∴过x+y+1=0与2x+3y+6=0的交点,且与2x-y+5=0垂直的直线的方程为:y+4=-$\frac{1}{2}$(x-3),
整理,得:x+2y+5=0.
(2)∵圆经过点A(0,0)和B(1,1),且圆心在x轴上,
∴设圆心(a,0),则$\sqrt{{a}^{2}}=\sqrt{(a-1)^{2}+(0-1)^{2}}$,
解得a=1,∴圆心(1,0),半径r=$\sqrt{{1}^{2}}$=1,
∴所求的圆的方程为(x-1)2+y2=1.
点评 本题考查直线方程与圆的方程的求法,是基础题,解题时要认真审题,注意点斜式方程的两点间距离公式的合理运用.

练习册系列答案
相关题目
2.如图1,已知正方体ABCD-A1B1ClD1的棱长为a,动点M、N、Q分别在线段PM上.当三棱锥Q-BMN的俯视图如图2所示时,三棱锥Q-BMN的正视图面积等于( )


| A. | $\frac{1}{2}$a2 | B. | $\frac{1}{4}$a2 | C. | $\frac{\sqrt{2}{a}^{2}}{4}$ | D. | $\frac{\sqrt{3}{a}^{2}}{4}$ |
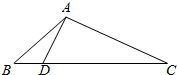 如图△ABC中,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,又己知BC边上有一点D,使∠DAC=90°,BD=$\sqrt{3}$.
如图△ABC中,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,又己知BC边上有一点D,使∠DAC=90°,BD=$\sqrt{3}$.