Question

15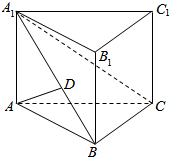．在值三棱柱ABC-A₁B₁C₁中，AD⊥平面A₁BC，其垂足D落在A₁B上．
（1）求证：BC⊥A₁B；
（2）若V_ABC-A1B1C1=3$\sqrt{3}$，BC=2，∠BA₁C=$\frac{π}{6}$，求三棱锥A₁-ABC的体积及AD长．

Answer 1

分析 （1）由AD⊥平面A₁BC可知AD⊥BC，由A₁A⊥平面ABC可知A₁A⊥BC，故BC⊥平面A₁AB，从而推出BC⊥A₁B；
（2）三棱锥A₁-ABC与三棱柱ABC-A₁B₁C₁同底同高，故三棱锥A₁-ABC的体积等于三棱柱ABC-A₁B₁C₁体积的$\frac{1}{3}$，由（1）证明可得△A₁BC是直角三角形，结合∠BA₁C=$\frac{π}{6}$，BC=2可求得A₁B的长，由棱锥的体积可得到A₁A•AB的值，由A₁A•AB=A₁B•AD可解出AD．

解答 （1）证明：∵三棱柱ABC-A₁B₁C₁是直三棱柱，
∴A₁A⊥平面ABC，∵BC?平面ABC，
∴A₁A⊥BC，
∵AD⊥平面A₁BC，BC?平面ABC，
∴AD⊥BC，
又∵A₁A?平面A₁AB，AD?平面A₁AB，A₁A∩AD=A，
∴BC⊥平面A₁AB，∵A₁B?平面A₁AB，
∴BC⊥A₁B．
（2）解∵若V_{棱柱ABC-A1B1C1}=S_△ABC•A₁A=3$\sqrt{3}$，
∴V${\;}_{棱锥{A}_{1}-ABC}$=$\frac{1}{3}$S_△ABC•A₁A=$\sqrt{3}$．
由（1）可知BC⊥平面A₁AB，AB?平面A₁AB，
∴AB⊥BC，
∴V${\;}_{棱锥{A}_{1}-ABC}$=$\frac{1}{3}$S_△ABC•A₁A=$\frac{1}{6}$×AB×BC×A₁A=$\sqrt{3}$．
∴A₁A•AB=3$\sqrt{3}$，
∵BC⊥A₁B，BC=2，∠BA₁C=$\frac{π}{6}$，
∴A₁C=2BC=4，A₁B=$\sqrt{{A}_{1}{C}^{2}-B{C}^{2}}$=2$\sqrt{3}$，
∵A₁A⊥平面ABC，AB?平面ABC，
∴A₁A⊥AB，
∵S${\;}_{△{A}_{1}AB}$=$\frac{1}{2}$A₁A•AB=$\frac{1}{2}$A₁B•AD，
∴AD=$\frac{{A}_{1}A•AB}{{A}_{1}B}$=$\frac{3}{2}$．

点评 本题考查了线面垂直的性质与判断，几何体体积计算，寻求垂直关系是解题关键．