题目内容

5．已知点P1（x1，2015）和P2（x2，2015）在二次函数f（x）=ax2+bx+24的图象上，则f（x1+x2）的值为24．

分析 先把P1点与P2点坐标代入二次函数解析式得ax12+bx1+24=2015，ax22+bx2+24=2015，两式相减得到a（x12-x22）+b（x1-x2）=0，而x1≠x2，所以a（x1+x2）+b=0，即x1+x2=-$\frac{b}{a}$，然后把x=-$\frac{b}{a}$ 代入f（x）=ax2+bx+24进行计算即可

解答 解：∵P1（x1，2015）和P2（x2，2015）是二次函数f（x）=ax2+bx+24（a≠0）的图象上两点，∴ax12+bx1+24=2015，ax22+bx2+24=2015，
∴a（x12-x22）+b（x1-x2）=0，
∵x1≠x2，
∴a（x1+x2）+b=0，即x1+x2=-$\frac{b}{a}$，
把x=-$\frac{b}{a}$ 代入f（x）=ax2+bx+24（a≠0）得f（x）=a×（-$\frac{b}{a}$ ）2+b×（-$\frac{b}{a}$）+24=24．
故答案为：24．

点评 本题考查了二次函数图象上点的坐标特征：二次函数f（x）=ax2+bx+c的图象上点的坐标满足其解析式．

练习册系列答案
相关题目
15．已知单调递增的等比数列{an}满足：a2+a4=20，且a3+2是a2，a4的等差中项．
（1）求数列{an}的通项公式；
（2）若bn=anlog${\;}_{\frac{1}{2}}$an，Sn=b1+b2+…+bn，求使Sn+n•2n+1＞50成立的正整数n的最小值．
16．已知定义域为R的函数f（x）=$\frac{b-{2}^{-x}}{{2}^{-x+1}+2}$是奇函数．
（1）求b的值；
（2）判断并证明函数f（x）的单调性；
（3）若对任意的t∈R，不等式f（t2-2t）+f（2t2-k）＜0有解，求k的取值范围．
13．已知{an}是等差数列，a1=1，公差d≠0，Sn为其前n项和，若a1，a2，a5成等比数列，则S8=（　　）
A．35B．50C．62D．64
20．（1）已知x$＜\frac{5}{4}$，求函数y=4x-2+$\frac{1}{4x-5}$的最大值．
（2）已知a≤1且a≠0，解关于x的二次不等式ax2-2x-2ax+4＞0．
10．定义：对于函数f（x），若在定义域内存在实数x，满足f（-x）=-f（x），则称f（x）为“局部奇函数”．
（1）已知二次函数f（x）=ax2+2x-4a（a∈R），试判断f（x）是否为定义域R上的“局部奇函数”？若是，求出满足f（-x）=-f（x）的x的值；若不是，请说明理由；
（2）若f（x）=2x+m是定义在区间[-1，1]上的“局部奇函数”，求实数m的取值范围．
17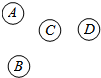．如图所示，A，B，C，D是海上的四个小岛，要建三座桥，将这四个岛连接起来，则不同的建桥方案共有（　　）
A．48种B．32种C．24种D．16种
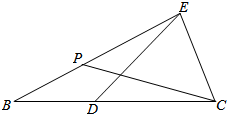14．已知在△BCE中，D是边BC上一点，满足CD=2BD=2CE=4，P是边BE上一点．满足∠BPD=∠DCE=60°．
（1）求证：P，D，C，E四点共圆，并求其外接圆的面积；
（2）求BP的长．
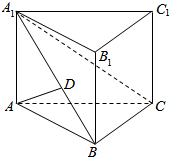15．在值三棱柱ABC-A1B1C1中，AD⊥平面A1BC，其垂足D落在A1B上．
（1）求证：BC⊥A1B；
（2）若VABC-A1B1C1=3$\sqrt{3}$，BC=2，∠BA1C=$\frac{π}{6}$，求三棱锥A1-ABC的体积及AD长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网