题目内容
3. 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)的部分图象如图所示,则函数解析式为y=4sin($\frac{π}{8}$x-$\frac{3π}{4}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π,x∈R)的部分图象如图所示,则函数解析式为y=4sin($\frac{π}{8}$x-$\frac{3π}{4}$).
分析 由题意易得A和ω值,代入点(6,0)可得φ值,验证可得.
解答 解:由题意和图象可得A=4,
函数的周期T=$\frac{2π}{ω}$=2(6+2),
解得ω=$\frac{π}{8}$,故y=4sin($\frac{π}{8}$x+φ),
代入点(6,0)可得0=4sin($\frac{3π}{4}$+φ),
∴$\frac{3π}{4}$+φ=kπ,k∈Z,
结合|φ|<π可得φ=-$\frac{3π}{4}$或φ=$\frac{π}{4}$,
当φ=$\frac{π}{4}$时,y=4sin($\frac{π}{8}$x+$\frac{π}{4}$),
由图象可知当x取很小的正角时,函数值y为负值,不合题意,舍去;
故y=4sin($\frac{π}{8}$x-$\frac{3π}{4}$)
故答案为:y=4sin($\frac{π}{8}$x-$\frac{3π}{4}$)
点评 本题考查三角函数的图象,数形结合是解决问题的关键,属基础题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
13.已知{an}是等差数列,a1=1,公差d≠0,Sn为其前n项和,若a1,a2,a5成等比数列,则S8=( )
| A. | 35 | B. | 50 | C. | 62 | D. | 64 |
11.a=tan(cos(-1))与b=cos(tan(-1))的大小关系为( )
| A. | a>b | B. | a<b | C. | a=b | D. | 均不对 |
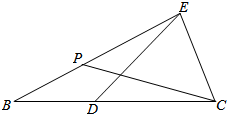 已知在△BCE中,D是边BC上一点,满足CD=2BD=2CE=4,P是边BE上一点.满足∠BPD=∠DCE=60°.
已知在△BCE中,D是边BC上一点,满足CD=2BD=2CE=4,P是边BE上一点.满足∠BPD=∠DCE=60°.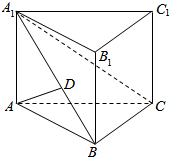 在值三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在A1B上.
在值三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在A1B上.