题目内容
4.设△ABC的面积S=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{4}$,角A,B,C所对的边为a,b,c且c=$\sqrt{2}$a.(1)求角C的大小;
(2)若△ABC内一点P满足AP=AC,BP=CP,求∠PAC的大小.
分析 (1)根据三角形的面积公式和余弦定理,即可即可求出A的大小,再根据正弦定理求出C的大小,
(2)首先确定P的位置,由(1)△ABC为等腰直角三角形,以A点为坐标原点,以斜边BC为x轴,建立如何所示的坐标系,作BC的垂直平分线,DE,交圆于点P,分别表示各点的坐标,求出直线DE的方程,联立圆的方程求出点P的坐标,再分别表示出$\overrightarrow{AC}$,$\overrightarrow{AP}$,利用向量的数量积即可求出cos∠PAC,问题得以解决.
解答 解:(1)∵S=$\frac{1}{2}$bcsinA,b2+c2-a2=2bccosA,
∴S=$\frac{1}{4}$(a2+b2-c2)变形得:$\frac{1}{2}$absinC=$\frac{1}{4}$×2bccosA,
整理得:tanA=1,
又0<A<π,
则A=$\frac{π}{4}$,
∵c=$\sqrt{2}$a,
∴sinC=$\sqrt{2}$sinA=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=1,
又0<C<π,
∴C=$\frac{π}{2}$,
(2)由(1)△ABC为等腰直角三角形,
以A点为坐标原点,以斜边BC为x轴,建立如何所示的坐标系,
作BC的垂直平分线,DE,交圆于点P,
∴PC=PB,AC=AP,
∴点P就是所求的点,
设半径为$\sqrt{2}$,则AB=2,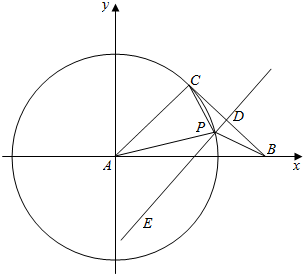
则圆的方程为x2+y2=2,①
∴A(0,0),C(1,1),B(2,0),
∴D($\frac{3}{2}$,$\frac{1}{2}$),
∵kED=KAC=tan$\frac{π}{4}$=1,
∴直线ED的方程为y-$\frac{1}{2}$=x-$\frac{3}{2}$,即x-y-1=0,②
由①②构成方程组,则为$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=2}\\{x-y-1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{1+\sqrt{3}}{2}}\\{y=\frac{-1+\sqrt{3}}{2}}\end{array}\right.$,或$\left\{\begin{array}{l}{x=\frac{1-\sqrt{3}}{2}}\\{y=\frac{-1-\sqrt{3}}{2}}\end{array}\right.$(舍去),
∴点P的坐标为($\frac{1+\sqrt{3}}{2}$,$\frac{-1+\sqrt{3}}{2}$),
∴$\overrightarrow{AC}$=(1,1),$\overrightarrow{AP}$=($\frac{1+\sqrt{3}}{2}$,$\frac{-1+\sqrt{3}}{2}$),|$\overrightarrow{AC}$|=|$\overrightarrow{AP}$|=$\sqrt{2}$,
∴$\overrightarrow{AC}$•$\overrightarrow{AP}$=$\frac{1+\sqrt{3}}{2}$+$\frac{-1+\sqrt{3}}{2}$=$\sqrt{3}$,
∴cos∠PAC=$\frac{\overrightarrow{AC}•\overrightarrow{AP}}{|\overrightarrow{AC}||\overrightarrow{AP}|}$=$\frac{\sqrt{3}}{2}$,
∴∠PAC=$\frac{π}{6}$
点评 本题考查学生灵活运用三角形的面积公式及余弦定理、正弦定理化简求值,以及用解析几何的和向量的问题解决平面几何的问题,属于中档题.

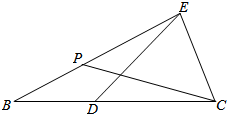 已知在△BCE中,D是边BC上一点,满足CD=2BD=2CE=4,P是边BE上一点.满足∠BPD=∠DCE=60°.
已知在△BCE中,D是边BC上一点,满足CD=2BD=2CE=4,P是边BE上一点.满足∠BPD=∠DCE=60°.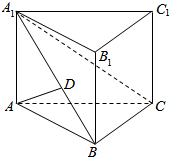 在值三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在A1B上.
在值三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在A1B上.