题目内容
对于任意的实数a,b,记max{a,b}=
.若F(x)=max{f(x),g(x)}(x∈R),其中函数y=f(x)(x∈R)是奇函数,且当x≥0时,f(x)=(x-1)2-2;函数y=g(x)(x∈R)是正比例函数,其图象与x≥0时函数y=f(x)的图象如图所示,则下列关于函数y=F(x)的说法中,正确的是( )
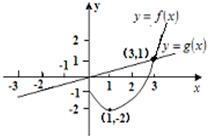
|
| A.y=F(x)为奇函数 |
| B.y=F(x)在(-3,0)上为增函数 |
| C.y=F(x)的最小值为-2,最大值为2 |
| D.以上说法都不正确 |

∵f(x)*g(x)=min{f(x),g(x)},
∴f(x)*g(x)=max{f(x),g(x)}的定义域为R,
f(x)*g(x)=min{f(x),g(x)},画出其图象如图中实线部分,
由图象可知:y=F(x)的图象不关于原点对称,不为奇函数;
y=F(x)在(-3,0)上不为增函数;
y=F(x)的没有最小值和最大值为,
故选D.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目