题目内容
在空间坐标系中的点M（x，y，z），若它的柱坐标为(3，
，3)，则它的球坐标为（ ）
| π |
| 3 |
A．(3，
| B．(3
| C．(3，
| D．(3
|
∵M点的柱面坐标为M(3，
，3)，设点M的直角坐标为（x，y，z），
∴x=3cos
=
，y=3sin
=
，z=3．
∴M点的直角坐标为：M（
，
，3）．
设点M的球面坐标系的形式为（r，φ，θ），r是球面半径，φ为向量OM在xOy面上投影到x正方向夹角，θ为向量OM与z轴正方向夹角，
∴r=
=3
，容易知道φ=60°=
，同时结合点M的直角坐标为（
，
，3）．
可知cosθ=
=
=
，
∴θ=
，
∴球面坐标为（3
，
，
）
故选：B．
| π |
| 3 |
∴x=3cos
| π |
| 3 |
| 3 |
| 2 |
| π |
| 3 |
3
| ||
| 2 |
∴M点的直角坐标为：M（
| 3 |
| 2 |
3
| ||
| 2 |
设点M的球面坐标系的形式为（r，φ，θ），r是球面半径，φ为向量OM在xOy面上投影到x正方向夹角，θ为向量OM与z轴正方向夹角，
∴r=
|
| 2 |
| π |
| 3 |
| 3 |
| 2 |
3
| ||
| 2 |
可知cosθ=
| z |
| r |
| 3 | ||
3
|
| ||
| 2 |
∴θ=
| π |
| 4 |
∴球面坐标为（3
| 2 |
| π |
| 3 |
| π |
| 4 |
故选：B．
练习册系列答案
阅读快车系列答案
相关题目
．
，
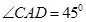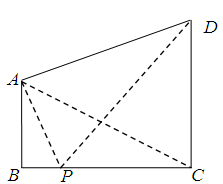
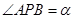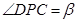，问点P在何处时，
最小？
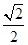，这样的点P的个数是( )