题目内容
如图,两座建筑物AB,CD的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9m和15m,从建筑物AB的顶部A看建筑物CD的张角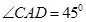 .
.
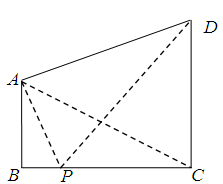
(1)求BC的长度;
(2)在线段BC上取一点P(点P与点B,C不重合),从点P看这两座建筑物的张角分别为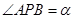 ,
,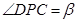 ,问点P在何处时,
,问点P在何处时,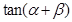 最小?
最小?
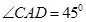 .
.
(1)求BC的长度;
(2)在线段BC上取一点P(点P与点B,C不重合),从点P看这两座建筑物的张角分别为
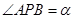 ,
,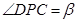 ,问点P在何处时,
,问点P在何处时,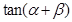 最小?
最小?(1)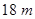 ;(2)
;(2)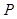 在距离
在距离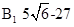 时,
时,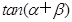 最小
最小
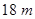 ;(2)
;(2)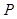 在距离
在距离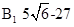 时,
时,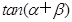 最小
最小试题分析:(1)由题意不难想到作
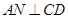 于
于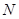 ,这样能将条件很好的集中在
,这样能将条件很好的集中在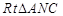 和
和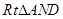 中,不妨设出一长度和角度,即设
中,不妨设出一长度和角度,即设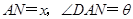 ,在上述两直角三角形中,由直角三角形中正切的含义即
,在上述两直角三角形中,由直角三角形中正切的含义即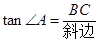 ,这样就可得到关于
,这样就可得到关于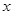 的一元二次方程,就可解得
的一元二次方程,就可解得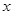 值; (2)先在图中含有
值; (2)先在图中含有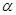 和
和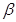 的两个直角三角形中,得到
的两个直角三角形中,得到 ,再由两角和的正切公式
,再由两角和的正切公式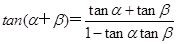 可求出
可求出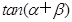 关于
关于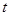 的表达式,通过化简得
的表达式,通过化简得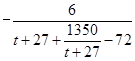 ,结合基本不等式可求出它的最小值,并由基本不等式成立的条件得到此时
,结合基本不等式可求出它的最小值,并由基本不等式成立的条件得到此时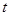 的值,即可确定出
的值,即可确定出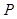 的位置.
的位置.试题解析:解:(1)如图作
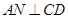 于
于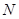 .
.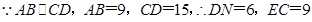 .
.设
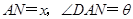 ,
,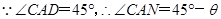 .
.在
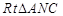 和
和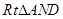 中,
中,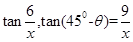 4分
4分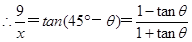
化简整理得
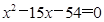 ,
,解得
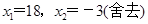 .
.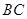 的长度是
的长度是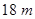 . 7分
. 7分(2)设
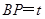 ,所以
,所以 9分
9分则
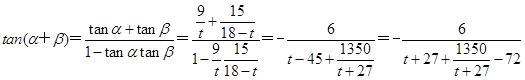 14分
14分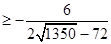 当且仅当
当且仅当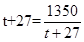 ,即
,即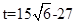 时,
时,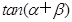 最小. 15分
最小. 15分答:
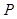 在距离
在距离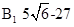 时,
时,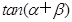 最小. 16分
最小. 16分
练习册系列答案
相关题目
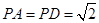 ,
,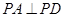 ,底面
,底面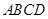 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD, 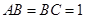 ,O为AD中点.
,O为AD中点.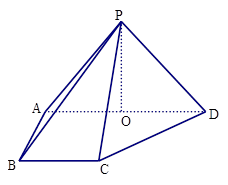
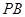 与平面
与平面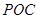 所成角的余弦值;
所成角的余弦值;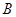 点到平面
点到平面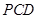 的距离;
的距离;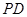 上是否存在一点
上是否存在一点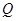 ,使得二面角
,使得二面角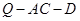 的余弦值为
的余弦值为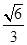 ?若存在,求出
?若存在,求出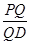 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.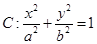
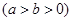 经过点
经过点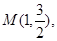 其离心率为
其离心率为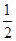 .
. 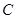 的方程;
的方程;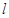 与椭圆
与椭圆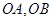 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 为坐标原点.求
为坐标原点.求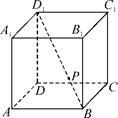
 的半径为
的半径为 ,
,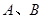 是球面上两点,
是球面上两点,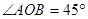 ,则
,则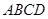 中,
中,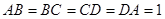 ,若
,若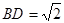 ,则
,则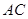 的取值范围是________.
的取值范围是________.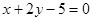 的距离
的距离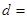 .
.