Question

【题目】已知a，b，c为正数，f（x）＝|x+a|+|x+b|+|x﹣c|.

（1）若a＝b＝c＝1，求函数f（x）的最小值；

（2）若f（0）＝1且a，b，c不全相等，求证：b3c+c3a+a3b＞abc.

Answer 1

【答案】（1）最小值2（2）证明见解析

【解析】

（1）法1：去绝对值，化为分段函数，求出最值，

法2：根据绝对值三角不等式，求出最值，

（2）法1：根据基本不等式即可证明，

法2：根据柯西不等式即可证明.

（1）因为a＝b＝c＝1，

所以f（x）＝|x+a|+|x+b|+|x﹣c|＝2|x+1|+|x﹣1|，

法1：由上可得：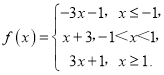

所以，当x＝﹣1时，函数f（x）的最小值为2；

法2：f（x）＝|x+a|+|x+b|+|x﹣c|＝|x+1|+|x+1|+|x﹣1|≥|x+1|+|x+1﹣x+1|＝2+|x+1|≥2，

当且仅当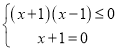，即x＝﹣1时取得最小值2；

（2）因为a，b，c为正数，所以要证b3c+c3a+a3b.，

即证明就行了，

法1：因为2222（a+b+c），当且仅当a＝b＝c时取等号.

又因为f（0）＝1即a+b+c＝1且a，b，c不全相等，

所以，

即b3c+c3a+a3b，

法2：因为（a+b+c），当且仅当取等号，

又因为f（0）＝1即a+b+c＝1且a，b，c不全相等，

所以，

即b3c+c3a+a3b.