题目内容
【题目】四棱锥S-ABCD中,底面ABCD是边长为2的菱形,![]() ,
,![]() ,二面角S-BD-C的余弦值为
,二面角S-BD-C的余弦值为![]() .
.
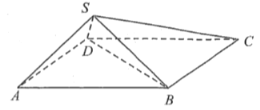
(I)证明:平面![]() 平面SBD;
平面SBD;
(Ⅱ)求二面角A-SD-C的余弦值.
【答案】(I)见解析(Ⅱ)![]()
【解析】
(I) 连接AC,交BD于点O.连接SO易证得![]() ,
,![]() 即
即![]() 平面SAO,得到
平面SAO,得到![]() ,利用余弦定理解得
,利用余弦定理解得![]() ,由
,由![]() 可证得
可证得![]() ,即可得到
,即可得到![]() 平面SBD,即可证得结论;
平面SBD,即可证得结论;
(Ⅱ)建系,设![]() 和
和![]() 分别为平面SAD、平面SCD的法向量,求出法向量,利用公式计算即可得出结果.
分别为平面SAD、平面SCD的法向量,求出法向量,利用公式计算即可得出结果.
(Ⅰ)连接AC,交BD于点O.连接SO菱形ABCD中,![]() ,且O是AC和BD的中点.
,且O是AC和BD的中点.
因为![]() ,所以
,所以![]() ,
,
![]() 是二面角S-BD-C的平面角,
是二面角S-BD-C的平面角,
即![]() ,
,![]() .
.
又![]() ,所以
,所以![]() 平面SAC,
平面SAC,![]() .
.
![]() 中,由余弦定理知:
中,由余弦定理知:
![]() .
.
所以![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() 平面SBD,
平面SBD,
又![]() 平面SAB,所以平面SAB⊥平面SBD.
平面SAB,所以平面SAB⊥平面SBD.
(Ⅱ)如图,分别以![]() ,
,![]() 为x,y轴的正方向,建立空间直角坐标系
为x,y轴的正方向,建立空间直角坐标系![]() .
.
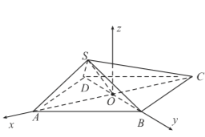
则点![]() ,
,![]()
![]()
![]()
 ,
,
![]() ,
,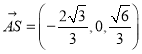 ,
,
![]() ,
, .
.
设![]() 和
和![]() 分别为平面SAD、平面SCD的法向量,
分别为平面SAD、平面SCD的法向量,
则由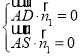 ,得
,得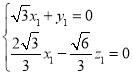 ,
,
取![]() ,
,
由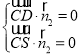 ,得
,得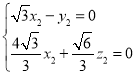 .
.
取![]() .
.
 .
.
故二面角A-SD-C的余弦值为![]() .
.

【题目】甘肃省是土地荒漠化较为严重的省份,一代代治沙人为了固沙、治沙,改善生态环境,不断地进行研究与实践,实现了沙退人进.![]() 年,古浪县八步沙林场“六老汉”三代人治沙群体作为优秀代表,被中宣部授予“时代楷模”称号.在治沙过程中为检测某种固沙方法的效果,治沙人在某一实验沙丘的坡顶和坡腰各布设了
年,古浪县八步沙林场“六老汉”三代人治沙群体作为优秀代表,被中宣部授予“时代楷模”称号.在治沙过程中为检测某种固沙方法的效果,治沙人在某一实验沙丘的坡顶和坡腰各布设了![]() 个风蚀插钎,以测量风蚀值.(风蚀值是测量固沙效果的指标之一,数值越小表示该插钎处被风吹走的沙层厚度越小,说明固沙效果越好,数值为
个风蚀插钎,以测量风蚀值.(风蚀值是测量固沙效果的指标之一,数值越小表示该插钎处被风吹走的沙层厚度越小,说明固沙效果越好,数值为![]() 表示该插钎处没有被风蚀)通过一段时间的观测,治沙人记录了坡顶和坡腰全部插钎测得的风蚀值(所测数据均不为整数),并绘制了相应的频率分布直方图.
表示该插钎处没有被风蚀)通过一段时间的观测,治沙人记录了坡顶和坡腰全部插钎测得的风蚀值(所测数据均不为整数),并绘制了相应的频率分布直方图.
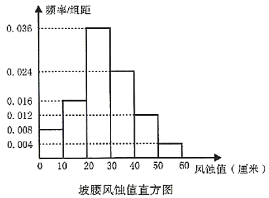
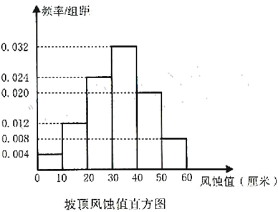
(Ⅰ)根据直方图估计“坡腰处一个插钎风蚀值小于![]() ”的概率;
”的概率;
(Ⅱ)若一个插钎的风蚀值小于![]() ,则该数据要标记“
,则该数据要标记“![]() ”,否则不标记根据以上直方图,完成列联表:
”,否则不标记根据以上直方图,完成列联表:
标记 | 不标记 | 合计 | |
坡腰 | |||
坡顶 | |||
合计 |
并判断是否有![]() 的把握认为数据标记“
的把握认为数据标记“![]() ”与沙丘上插钎所布设的位置有关?
”与沙丘上插钎所布设的位置有关?
附: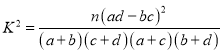 .
.
|
|
|
|
|
|
|
|