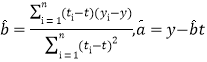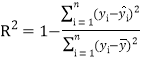题目内容
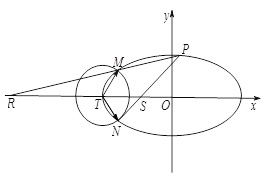
【题目】【2017银川一中模拟】如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=![]() CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
CD=1.现以AD为一边向梯形外作矩形ADEF,然后沿边AD将矩形ADEF翻折,使平面ADEF与平面ABCD垂直.
(1)求证:BC⊥平面BDE;
(2)若点D到平面BEC的距离为![]() ,求三棱锥F-BDE的体积.
,求三棱锥F-BDE的体积.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
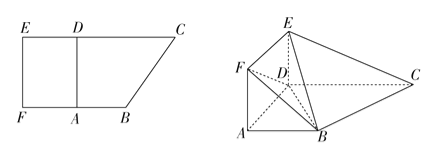
【解析】(1)证明:在矩形ADEF中,ED⊥AD,因为平面ADEF⊥平面ABCD,
所以 ED⊥平面ABCD,所以ED⊥BC. 又在直角梯形ABCD中,
AB=AD=1,CD=2,∠BDC=45°,所以BC=![]() ,
,
在△BCD中,BD=BC=![]() ,CD=2,
,CD=2,
所以BD2+BC2=CD2, 所以BC⊥BD,所以BC⊥平面BDE.
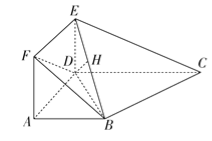
(2)由(1)得,平面DBE⊥平面BCE,作DH⊥BE于点H,
则DH⊥平面BCE,所以DH=![]() .在△BDE中,BD·DE=BE·DH,
.在△BDE中,BD·DE=BE·DH,
即![]() ·DE=
·DE=![]() (
(![]() ),解得DE=1.所以VF-BDE=VB-EFD=
),解得DE=1.所以VF-BDE=VB-EFD=![]() ×
×![]() ×1×1×1=
×1×1×1=![]() .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目