题目内容
正项数列{an}的前n项和Sn满足: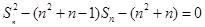
(1)求数列{an}的通项公式an;
(2)令 ,数列{bn}的前n项和为Tn.证明:对于任意n
,数列{bn}的前n项和为Tn.证明:对于任意n 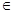 N*,都有Tn<
N*,都有Tn<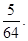
(1)2n (2)见解析
解析

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
题目内容
正项数列{an}的前n项和Sn满足: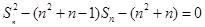
(1)求数列{an}的通项公式an;
(2)令 ,数列{bn}的前n项和为Tn.证明:对于任意n
,数列{bn}的前n项和为Tn.证明:对于任意n 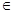 N*,都有Tn<
N*,都有Tn<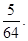
(1)2n (2)见解析
解析

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案