Question

【题目】已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2﹣x；

（1）求函数f（x）的解析式；

（2）求不等式f（x）＜0的解集．

Answer 1

【答案】（1），f（x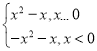）=,（2）{x|x＜﹣1或0＜x＜1}

【解析】

（1）设x＜0，则﹣x＞0，由当x≥0时，f（x）=x2﹣x，将﹣x＞0代入解析式，由奇偶性即可求解.

（2）由（1）分段解不等式，再取并集即可.

（1）设x＜0，则﹣x＞0，∵当x≥0时，f（x）=x2﹣x，

∴f（﹣x）=x2+x，

∵f（x）是定义在R上的奇函数，

∴f（x）=﹣f（﹣x）=﹣x2﹣x，

∴当x＜0时，f（x）=﹣x2﹣x，

综上所述，f（x）=；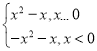

（2）当x≥0时，f（x）=x2﹣x＜0，∴0＜x＜1；

当x＜0时，f（x）=﹣x2﹣x＜0，∴x＜﹣1或x＞0，∴x＜﹣1，

综上所述，不等式f（x）＜0的解集为{x|x＜﹣1或0＜x＜1}．