题目内容
【题目】函数f′(x)是奇函数f(x)(x∈R)的导函数,f(1)=0,当x<0时,xf′(x)+f(x)>0,则使得f(x)<0成立的x的取值范围是( )
A.(﹣∞,﹣1)∪(0,1)
B.(﹣1,0)∪(1,+∞)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣1,0)∪(0,1)
【答案】B
【解析】解:设g(x)=xf(x),则g′(x)=xf′(x)+f(x),
∵当x<0时,xf′(x)+f(x)>0,
∴则当x<0时,g′(x)>0,
∴函数g(x)=xf(x)在(﹣∞,0)上为增函数,
∵函数f(x)是奇函数,∴g(﹣x)=(﹣x)f(﹣x)=(﹣x)[﹣f(x)]=xf(x)=g(x),
∴函数g(x)为定义域上的偶函数,
由f(1)=0得,g(1)=0,函数g(x)的图象大致如右图:
∵不等式f(x)<0 ![]() <0,
<0,
∴ ![]() 或
或 ![]() ,
,
由函数的图象得,﹣1<x<0或x>1,
∴使得f(x)<0成立的x的取值范围是:(﹣1,0)∪(1,+∞),
故选:B.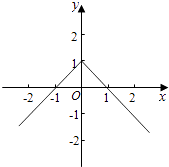
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

【题目】河南多地遭遇跨年霾,很多学校调整元旦放假时间,提前放假让学生们在家躲霾,郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动I级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |

(1)请在图中完成被调查人员年龄的频率分布直方图;
(2)若从年龄在![]() ,
, ![]() 两组采访对象中各随机选取2人进行深度跟踪调查,选中4人中不赞成这项举措的人数为
两组采访对象中各随机选取2人进行深度跟踪调查,选中4人中不赞成这项举措的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.