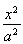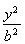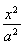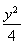题目内容
已知椭圆C1: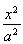 +
+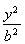 =1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
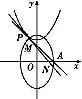
(1)求椭圆C1的方程;
(2)设点P在抛物线C2:y=x2+h(h∈R)上,C2在点P处的切线与C1交于点M,N.当线段AP的中点与MN的中点的横坐标相等时,求h的最小值.
【答案】
(1)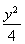 +x2=1 (2)1
+x2=1 (2)1
【解析】
解:(1)由题意,得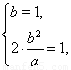
从而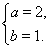
因此,所求的椭圆方程为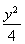 +x2=1.
+x2=1.
(2)设M(x1,y1),N(x2,y2),
P(t,t2+h),
则抛物线C2在点P处的切线斜率为
y′|x=t=2t,
直线MN的方程为:
y=2tx-t2+h.
将上式代入椭圆C1的方程中,
得4x2+(2tx-t2+h)2-4=0,
即4(1+t2)x2-4t(t2-h)x+(t2-h)2-4=0.①
因为直线MN与椭圆C1有两个不同的交点,
所以①式中的
Δ1=16[-t4+2(h+2)t2-h2+4]>0.②
设线段MN的中点的横坐标是x3,
则x3=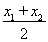 =
= .
.
设线段PA的中点的横坐标是x4,
则x4=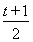 .
.
由题意,得x3=x4,
即t2+(1+h)t+1=0.③
由③式中的
Δ2=(1+h)2-4≥0,
得h≥1或h≤-3.
当h≤-3时,h+2<0,4-h2<0,
则不等式②不成立,
所以h≥1.
当h=1时,代入方程③得t=-1,
将h=1,t=-1代入不等式②,检验成立.
所以h的最小值为1.

练习册系列答案
相关题目