题目内容

下列四个命题中，真命题的个数为（　　）
①两个有公共起点且相等的向量，其终点可能不同；②若非零向量
AB
与
CD
是共线向量，则A、B、C、D四点共线；③若
a
∥
b
且
b
∥
c
，则
a
∥
c
；④四边形ABCD为平行四边形的充要条件是
AB
∥
DC
．
分析：（1）根据相等向量的定义判断①的真假
（2）根据共线向量的定义判断②的真假
（3）根据零向量的特征性质（平行于任意向量，且方向是任意的）判断③的真假
（4）根据四边形是平行四边形所满足的对边的关系（平行且相等）和平行向量的特点（不一定大小相等）可判断④的真假
解答：解：①相等向量是大小相等、方向相同的向量，如果两个相等向量起点相同，则由定义知终点必相同，∴命题①是假命题
②共线向量是基线平行或重合的向量，当非零向量
AB
，
CD
的基线平行时，这两个向量共线，但点A、B、C、D不共线，∴②是假命题
③当
b
=
0
时，
a
，
c
不一定平行，∴③是假命题
④
AB
∥
CD
时，四边形ABCD不一定是四边形，有可能是梯形．若要使四边形ABCD是平行四边形，应满足
AB
=
CD
，∴④是假命题
故选A
点评：本题考察相等向量、共线向量的有关知识，须掌握相等向量、共线向量的定义和特点．属简单题
练习册系列答案
相关题目
已知双曲线C：
x2
a2
-
y2
b2
=1满足条件：（1）焦点为F1（-5，0），F2（5，0）；（2）离心率为
5
3
，求得双曲线C的方程为f（x，y）=0．若去掉条件（2），另加一个条件求得双曲线C的方程仍为f（x，y）=0，则下列四个条件中，符合添加的条件可以是（　　）
①双曲线C：
x2
a2
-
y2
b2
=1上的任意点P都满足||PF1|-|PF2||=6；
②双曲线C：
x2
a2
-
y2
b2
=1的渐近线方程为4x±3y=0；
③双曲线C：
x2
a2
-
y2
b2
=1的焦距为10；
④双曲线C：
x2
a2
-
y2
b2
=1的焦点到渐近线的距离为4．
A、①③B、②③C、①④D、①②④
下列四个判断中，正确判断的个数为（　　）
①经过定点P（x0，y0）的直线都可以用y-y0=k（x-x0）表示；
②经过定点P（0，b）的直线都可以用y=kx+b表示；
③不经过原点的直线都可以用
x
a
+
y
b
=1表示；
④任意直线都可以用Ax+By+C=0（A，B不同时为零）表示．
（2012•厦门模拟）某赛季甲、乙两名篮球运动员各6场比赛得分情况用茎叶图记录，下列四个结论中，不正确的是（　　）
（如图，下列四个几何体中，它们各自的三视图（主视图、左视图、俯视图）有两个相同，而另一个不同的几何体是（　　）
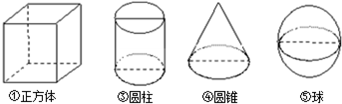
精英家教网
A、①②B、②③C、②④D、③④

已知命题：“”，命题：“”，给出下列四个判断：①是真命题，②是真命题，③是真命题，④是真命题，其中正确的是（     ）

A. ② ④               B. ② ③

C. ③ ④               D. ① ② ③

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网