题目内容
已知函数f(x)的定义域为R,若存在常数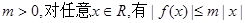 ,则称f(x)为F函数,给出下列函数:
,则称f(x)为F函数,给出下列函数:
①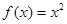 ;②
;②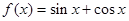 ;③
;③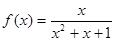 ;④f(x)是定义在R上的奇函数,且满足对一切实数
;④f(x)是定义在R上的奇函数,且满足对一切实数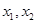 均有
均有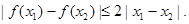 其中是F函数的序号为
其中是F函数的序号为
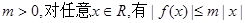 ,则称f(x)为F函数,给出下列函数:
,则称f(x)为F函数,给出下列函数:①
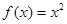 ;②
;②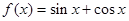 ;③
;③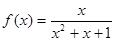 ;④f(x)是定义在R上的奇函数,且满足对一切实数
;④f(x)是定义在R上的奇函数,且满足对一切实数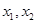 均有
均有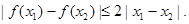 其中是F函数的序号为
其中是F函数的序号为| A.②④ | B.①③ | C.③④ | D.①② |
C
分析:本题是一个新定义的题目,故依照定义的所给的规则对所四个函数进行逐一验证,选出正确的即可.
解答:解:对于①,|f(x)|<m|x|,显然不成立,故其不是F函数;
对于②,f(x)=sinx+cosx,由于x=0时,|f(x)|<m|x|不成立,故不是F函数;
对于③,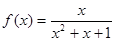 ,|f(x)|=
,|f(x)|=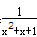 |x|≤
|x|≤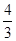 |x|,故对任意的m>
|x|,故对任意的m>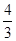 ,都有|f(x)|<m|x|,故其是F函数;
,都有|f(x)|<m|x|,故其是F函数;
对于④,f(x)是定义在R上的奇函数,且满足对一切实数x1,x2均有|f(x1)-f(x2)|≤2|x1-x2|,令x1=x,x2=0,由奇函数的性质知,f(0)=0,故有|f(x)|<2|x|.显然是F函数
故选C
解答:解:对于①,|f(x)|<m|x|,显然不成立,故其不是F函数;
对于②,f(x)=sinx+cosx,由于x=0时,|f(x)|<m|x|不成立,故不是F函数;
对于③,
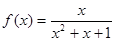 ,|f(x)|=
,|f(x)|=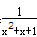 |x|≤
|x|≤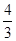 |x|,故对任意的m>
|x|,故对任意的m>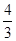 ,都有|f(x)|<m|x|,故其是F函数;
,都有|f(x)|<m|x|,故其是F函数;对于④,f(x)是定义在R上的奇函数,且满足对一切实数x1,x2均有|f(x1)-f(x2)|≤2|x1-x2|,令x1=x,x2=0,由奇函数的性质知,f(0)=0,故有|f(x)|<2|x|.显然是F函数
故选C

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
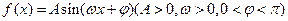 的一个周期的图象,如图(1)求
的一个周期的图象,如图(1)求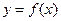 的解析式(2)若函数
的解析式(2)若函数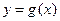 与
与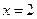 对称,求
对称,求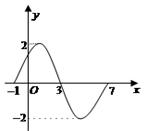
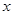 )的值域是
)的值域是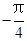 ,
,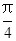 ] B [
] B [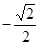 ,
,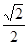 ] C [
] C [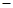 tan1 ,tan1] D [-1 ,1]
tan1 ,tan1] D [-1 ,1]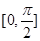 上的最大点是( )
上的最大点是( )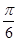
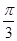
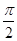
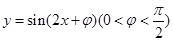 图象的一条对称轴在
图象的一条对称轴在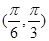 内,则满足此条件的一个
内,则满足此条件的一个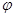 值为( )
值为( )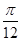
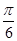
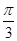
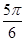
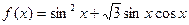
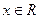
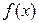 的最小正周期和值域;
的最小正周期和值域;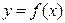 的图象按向量
的图象按向量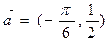 平移后得到函数
平移后得到函数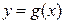 的图 象,求函数
的图 象,求函数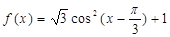 的最小正周期是( )
的最小正周期是( )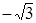
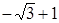
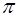
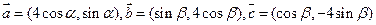
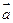 与
与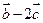 垂直,求
垂直,求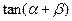 的值;
的值;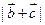 的最大值;
的最大值;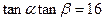 ,求证:
,求证: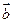 .
.