题目内容
设方程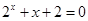 和方程
和方程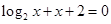 的根分别为
的根分别为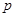 和
和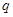 ,函数
,函数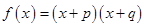
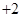 ,则( )
,则( )
A.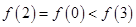 |
B.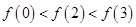 |
C.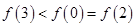 |
D.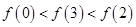 |
A
解析试题分析:令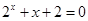 ,可得
,可得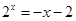 ,同理,令
,同理,令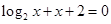 ,得
,得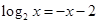 ,从而
,从而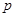 为曲线
为曲线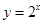 与直线
与直线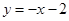 交点
交点 的横坐标,
的横坐标, 为曲线
为曲线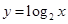 与直线
与直线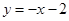 交点
交点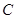 的横坐标,
的横坐标,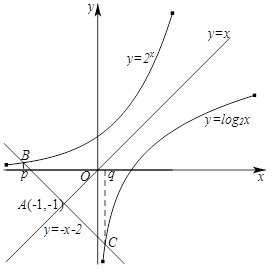
而曲线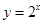 与曲线
与曲线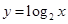 关于直线
关于直线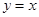 对称,故点
对称,故点 与点
与点 关于直线
关于直线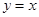 对称,由于直线
对称,由于直线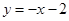 与直线
与直线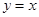 对称,故
对称,故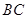 的中点
的中点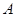 即为直线
即为直线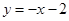 与直线
与直线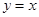 的交点,故点
的交点,故点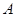 的坐标为
的坐标为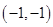 ,由中点坐标公式可得
,由中点坐标公式可得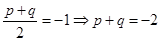 ,
,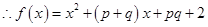
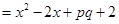 ,故曲线
,故曲线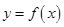 的对称轴为直线
的对称轴为直线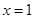 ,因此函数
,因此函数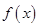 在
在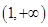 上单调递增,故有
上单调递增,故有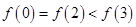 ,故选A.
,故选A.
考点:1.函数的零点;2.互为反函数的两个函数图象的关系;3.二次函数

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知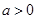 ,函数
,函数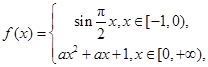 若
若 ,则实数
,则实数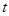 的取值范围为( )
的取值范围为( )
A.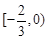 | B.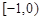 | C.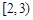 | D.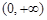 |
若函数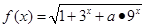 ,其定义域为
,其定义域为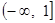 ,则
,则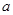 的取值范围是( )
的取值范围是( )
A.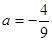 | B.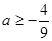 | C.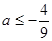 | D.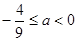 |
已知函数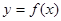 是定义在实数集R上的奇函数,且当
是定义在实数集R上的奇函数,且当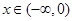 时
时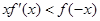 成立(其中
成立(其中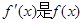 的导函数),若
的导函数),若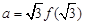 ,
,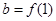 ,
,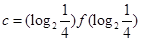 则
则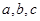 的大小关系是( )
的大小关系是( )
A.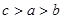 | B.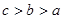 | C.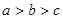 | D.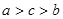 |
已知定义在 上的周期为
上的周期为 的偶函数
的偶函数 ,当
,当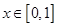 时,
时,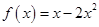 ,则
,则 在区间
在区间 内零点的个数为( )
内零点的个数为( )
| A.3019 | B.2020 | C.3021 | D.3022 |
设定义在R上的函数 是最小正周期为
是最小正周期为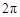 的偶函数,
的偶函数,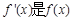 的导函数,当
的导函数,当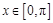 时,
时,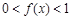 ;当
;当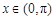 且
且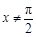 时,
时,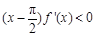 ,则方程
,则方程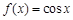 在
在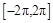 上的根的个数为( )
上的根的个数为( )
| A.2 | B.5 | C.8 | D.4 |
已知函数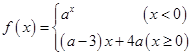 ,满足对任意
,满足对任意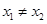 ,都有
,都有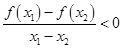 成立,则
成立,则 的取值范围是 ( )
的取值范围是 ( )
A.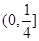 | B.(1,2] | C.(1,3) | D.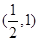 |
函数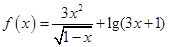 的定义域为( )
的定义域为( )
A. | B.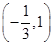 | C.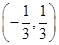 | D.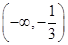 |
若函数 对于任意的
对于任意的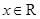 都有
都有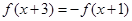 ,且
,且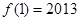 ,则
,则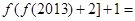 ( )
( )
A.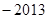 | B.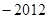 | C.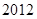 | D.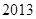 |