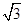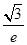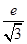题目内容
已知函数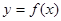 是定义在实数集R上的奇函数,且当
是定义在实数集R上的奇函数,且当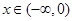 时
时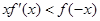 成立(其中
成立(其中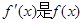 的导函数),若
的导函数),若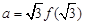 ,
,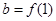 ,
,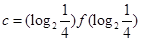 则
则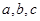 的大小关系是( )
的大小关系是( )
A.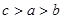 | B.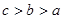 | C.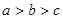 | D.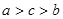 |
B
解析试题分析:设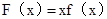 ,得
,得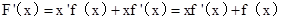 ,
,
∵当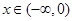 时,
时,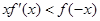 ,且
,且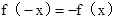
∴当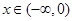 时,
时,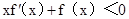 ,即
,即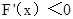
由此可得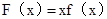 在区间
在区间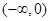 上是减函数,
上是减函数,
∵函数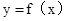 是定义在实数集R上的奇函数,
是定义在实数集R上的奇函数,
∴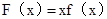 是定义在实数集R上的偶函数,在区间
是定义在实数集R上的偶函数,在区间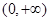 上
上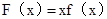 是增函数.
是增函数.
而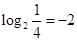 ,所以,
,所以,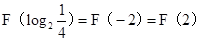 ,
,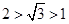 ,故
,故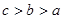 .选B.
.选B.
考点:应用导数研究函数的单调性、函数的奇偶性、函数值比较大小.

练习册系列答案
相关题目
已知函数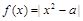 在
在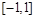 上的最大值为
上的最大值为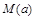 ,则
,则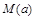 的最小值为( )
的最小值为( )
A.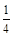 | B.1 | C.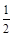 | D.2 |
已知函数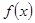 是定义在实数集R上的不恒为零的偶函数,且对任意实数
是定义在实数集R上的不恒为零的偶函数,且对任意实数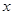 都有
都有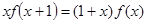 ,则
,则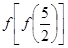 的值是( )
的值是( )
| A.0 | B.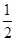 | C.1 | D.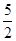 |
已知函数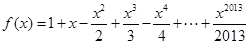 且函数
且函数 的零点均在区间
的零点均在区间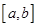
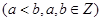 内,圆
内,圆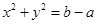 的面积的最小值是( )
的面积的最小值是( )
A.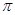 | B.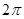 | C. | D.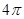 |
设方程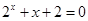 和方程
和方程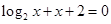 的根分别为
的根分别为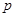 和
和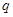 ,函数
,函数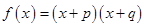
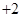 ,则( )
,则( )
A.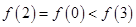 |
B.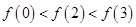 |
C.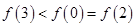 |
D.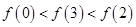 |
方程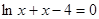 的解
的解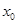 属于区间 ( )
属于区间 ( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.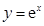 | B.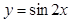 | C.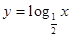 | D. |
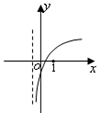
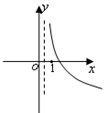
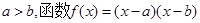 的图象如图,则函数
的图象如图,则函数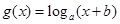 的图象可能为( )
的图象可能为( )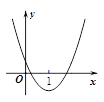
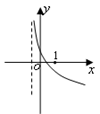
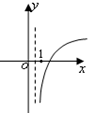
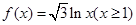 ,若将其图像绕原点逆时针旋转
,若将其图像绕原点逆时针旋转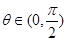 角后,所得图像仍是某函数的图像,则当角
角后,所得图像仍是某函数的图像,则当角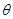 取最大值
取最大值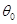 时,
时,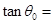 ( )
( )