题目内容
设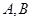 分别为椭圆
分别为椭圆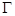 :
: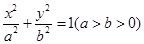 的左右顶点,
的左右顶点,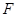 为右焦点,
为右焦点,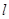 为
为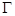 在点
在点 处的切线,
处的切线,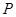 为
为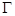 上异于
上异于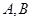 的一点,直线
的一点,直线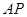 交
交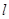 于
于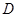 ,
,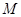 为
为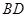 中点,有如下结论:①
中点,有如下结论:①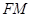 平分
平分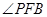 ;②
;②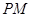 与椭圆
与椭圆 相切;③
相切;③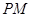 平分
平分 ;④使得
;④使得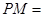
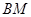 的点
的点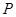 不存在.其中正确结论的序号是_____________.
不存在.其中正确结论的序号是_____________.
①②
解析试题分析:设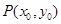 ,则
,则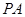 的方程为:
的方程为: ,令
,令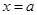 得
得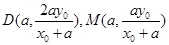 .
.
对①,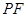 的方程为:
的方程为: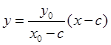 即
即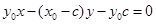 ,所以点M到直线PF的距离为
,所以点M到直线PF的距离为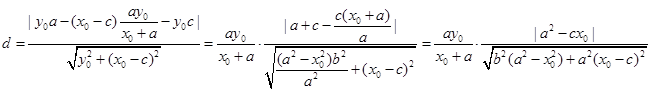
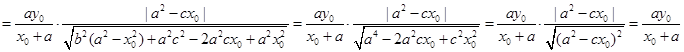 即点M到PF到距离等于M到FB的距离,所以
即点M到PF到距离等于M到FB的距离,所以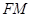 平分
平分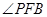 ,成立;对②,直线PM的斜率为
,成立;对②,直线PM的斜率为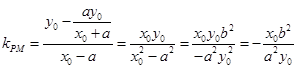 ,将
,将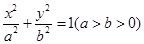 求导得
求导得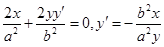 ,所以过点P的切线的斜率为
,所以过点P的切线的斜率为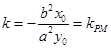 (也可用
(也可用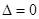 求得切线的斜率),所以椭圆
求得切线的斜率),所以椭圆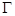 在点
在点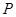 处的切线即为PM,②成立;对③,延长
处的切线即为PM,②成立;对③,延长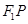 与直线
与直线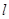 交于点
交于点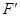 ,由椭圆的光学性质知,
,由椭圆的光学性质知,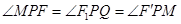 ,于是
,于是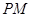 平分
平分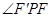 ,而不平分
,而不平分 ,故③不成立;
,故③不成立;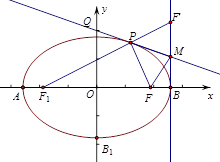
若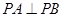 ,则
,则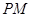 为
为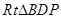 的斜边中线,
的斜边中线,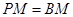 ,这样的
,这样的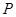 有4个,故④不成立.
有4个,故④不成立.
考点:1、椭圆;2、椭圆的切线;3、角平分线.

练习册系列答案
相关题目
 分别为双曲线
分别为双曲线 的左、右焦点,若在双曲线右支上存在点P,满足
的左、右焦点,若在双曲线右支上存在点P,满足 ,则该双曲线的渐近线方程为 .
,则该双曲线的渐近线方程为 .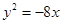 的焦点与双曲线
的焦点与双曲线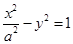 的左焦点重合,则双曲线的两条渐近线的夹角为 .
的左焦点重合,则双曲线的两条渐近线的夹角为 . 为双曲线
为双曲线 的两个焦点,点
的两个焦点,点 在双曲线上且
在双曲线上且 ,则
,则 的面积是
的面积是  的离心率为
的离心率为 ,则实数m的值为 .
,则实数m的值为 . 的左,右焦点分别为
的左,右焦点分别为 ,点P在双曲线的右支上,且
,点P在双曲线的右支上,且 ,则此双曲线的离心率e的取值范围是________.
,则此双曲线的离心率e的取值范围是________. 的焦点坐标是 .
的焦点坐标是 . =1(a>0,b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶3的两段,则此双曲线的离心率为________.
=1(a>0,b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶3的两段,则此双曲线的离心率为________.