题目内容
抛物线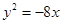
的焦点与双曲线
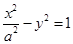的左焦点重合，则双曲线的两条渐近线的夹角为 .
解析试题分析：因为抛物线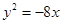的焦点为
所以
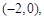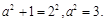所以双曲线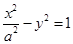的渐近线方程为
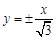，其夹角为.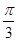
考点：双曲线的渐近线
练习册系列答案
高效智能课时作业系列答案
相关题目
高效智能课时作业系列答案题目内容
抛物线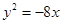的焦点与双曲线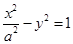的左焦点重合，则双曲线的两条渐近线的夹角为 .
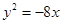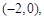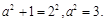解析试题分析：因为抛物线的焦点为所以所以双曲线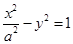的渐近线方程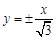为，其夹角为.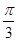
考点：双曲线的渐近线
高效智能课时作业系列答案
与圆x2+y2=a2+b2在第一象限的交点，其中F1,F2分别是双曲线的左、右焦点，且
，则双曲线的离心率为______.[来
到双曲线
的一条渐近线的距离为
，则双曲线
的离心率为 ．
分别为椭圆
:
的左右顶点,
为右焦点,
为
处的切线,
为
交
,
为
中点,有如下结论:①
平分
;②
与椭圆
;④使得
的点
的焦点坐标为_________________;
的焦点到双曲线
的渐近线的距离是 ．
＝1，过定点P(2，1)作直线交双曲线于P1、P2两点，并使P(2，1)为P1P2的中点，则此直线方程是____________．
的右焦点且与双曲线两支都相交，则双曲线离心率e的取值范围是