题目内容
若a,b是两个不共线的非零向量,t∈R.
(1)若a,b起点相同,t为何值时,a,tb,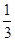 (a+b)三向量的终点在一直线上?
(a+b)三向量的终点在一直线上?
(2)若|a|=|b|且a与b夹角为60°,t为何值时,|a-tb|的值最小?
(1)若a,b起点相同,t为何值时,a,tb,
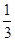 (a+b)三向量的终点在一直线上?
(a+b)三向量的终点在一直线上?(2)若|a|=|b|且a与b夹角为60°,t为何值时,|a-tb|的值最小?
(1)t=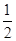 (2)当t=
(2)当t=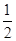 时,|a-tb|有最小值
时,|a-tb|有最小值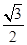 |a|
|a|
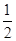 (2)当t=
(2)当t=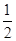 时,|a-tb|有最小值
时,|a-tb|有最小值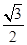 |a|
|a|本试题主要考查了向量的运算。
(1)设a-tb=m[a-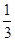 (a+b)],m∈R, 2分
(a+b)],m∈R, 2分
化简得(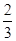 m-1)a=(
m-1)a=(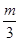 -t)b,
-t)b,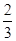 m-1=0且
m-1=0且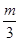 -t=0, 4分
-t=0, 4分
∴t=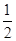 时,a,tb,
时,a,tb,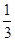 (a+b)的终点在一直线上. 6分
(a+b)的终点在一直线上. 6分
(2)|a-tb|2=(a-tb)2=|a|2+t2|b|2-2t|a||b|cos60°=(1+t2-t)|a|2. 8分
∴当t=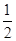 时,|a-tb|有最小值
时,|a-tb|有最小值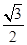 |a|.
|a|.
(1)设a-tb=m[a-
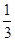 (a+b)],m∈R, 2分
(a+b)],m∈R, 2分化简得(
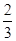 m-1)a=(
m-1)a=(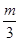 -t)b,
-t)b,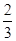 m-1=0且
m-1=0且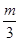 -t=0, 4分
-t=0, 4分∴t=
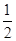 时,a,tb,
时,a,tb,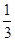 (a+b)的终点在一直线上. 6分
(a+b)的终点在一直线上. 6分(2)|a-tb|2=(a-tb)2=|a|2+t2|b|2-2t|a||b|cos60°=(1+t2-t)|a|2. 8分
∴当t=
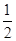 时,|a-tb|有最小值
时,|a-tb|有最小值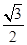 |a|.
|a|. 
练习册系列答案
相关题目
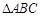 中,
中,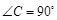 ,
, ,
,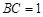 ,
, 为斜边
为斜边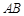 的中点,则
的中点,则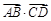 = .
= . ,
, ,
, 与
与 的夹角为
的夹角为 ,
, (2)求
(2)求 (3)若向量
(3)若向量 与
与 的值.
的值.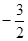

 ﹒
﹒
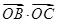 的最大值是( )
的最大值是( )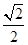 C.2 D.
C.2 D.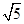
 的值为( )
的值为( )




 与向量
与向量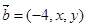 平行,则
平行,则 ▲ .
▲ .  ,
,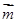 与
与 的夹角为
的夹角为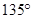 ,则
,则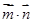 等于( )
等于( )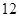
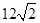
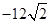
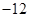
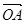 ·
· =6, △OAB的重心是G,则|
=6, △OAB的重心是G,则|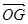 | 的最小值是( )
| 的最小值是( )