题目内容
12.设函数f(x)=$\left\{\begin{array}{l}{2^{1-x}},x≤1\\ 1-{log_2}x,x>1\end{array}$,则f(f(-2))=-2;满足不等式f(x)≤4的x的取值范围是{x|x≥-1}.分析 根据函数的解析式,先求得f(-2)的值,可得f(f(-2))的值. 把不等式f(x)≤4,转化为与之等价的2个不等式组,求得每个不等式组的解集,再取并集,即得所求.
解答 解:根据函数f(x)=$\left\{\begin{array}{l}{2^{1-x}},x≤1\\ 1-{log_2}x,x>1\end{array}$,可得f(-2)=23=8,∴f(f(-2))=f(8)=1-log28=1-3=-2.
不等式f(x)≤4,等价于$\left\{\begin{array}{l}{x≤1}\\{{2}^{1-x}{≤2}^{2}}\end{array}\right.$①,或$\left\{\begin{array}{l}{x>1}\\{1{-log}_{2}x≤4}\end{array}\right.$ ②.
解①求得-1≤x≤1;解②求得x>1,故不等式f(x)≤4的解集为{x|x≥-1},
故答案为:-2;{x|x≥-1}.
点评 本题主要考查分段函数的应用,求函数的值,指数、对数不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
20.设等差数列{an}的前n项和为Sn.若以a2,a4是方程x2-4x+3=0的两个根,则S5等于( )
| A. | -20 | B. | -10 | C. | 10 | D. | 20 |
1.已知f(x)=3-2x+x2,x∈{-1,1,0,2,3},则f(x)的值域为( )
| A. | {2,3,6} | B. | {1,2,3,6} | C. | {2,3,-3,6} | D. | {2,-2,3} |
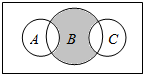 全集为1,A、B、C均为1的子集,则阴影部分表示的集合是(∁I(A∪C))∩B.
全集为1,A、B、C均为1的子集,则阴影部分表示的集合是(∁I(A∪C))∩B.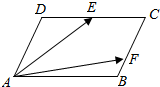 如图,平行四边形ABCD中,E为CD中点,F在线段BC上,且BC=3BF.已知$\overrightarrow{AD}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x的值为$\frac{6}{5}$.
如图,平行四边形ABCD中,E为CD中点,F在线段BC上,且BC=3BF.已知$\overrightarrow{AD}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x的值为$\frac{6}{5}$.