��Ŀ����
����Ŀ����֪��H��x0 �� y0����ԲC��x2+y2+Dx+Ey+F=0�����е�CΪԲ�ģ�D2+E2��4F��0���⣬�ɵ�H��ԲC�����ߣ�����һ���е�ΪM��
��֤��|HM|= ![]() ��
��
��1����֪��H��x0 �� y0����ԲC��x2+y2+Dx+Ey+F=0�����е�CΪԲ�ģ�D2+E2��4F��0���⣬�ɵ�H��ԲC�����ߣ�����һ���е�ΪM��
��֤��|HM|= ![]() ��
��
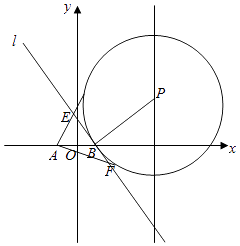
��2����ͼ��P��ֱ��x=4��һ���㣬��PΪԲ�ĵ�ԲP������B��1��0����ֱ��l��ԲP�ڵ�B�������ߣ���A����1��0����ԲP���������߷ֱ���l����E��F���㣮
��֤��|EA|+|EB|Ϊ��ֵ��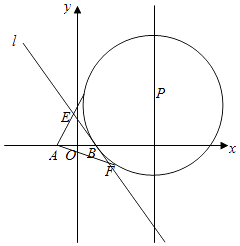
���𰸡�
��1��֤����ԲC�ķ���x2+y2+Dx+Ey+F=0��
��Ϊ������Ϊ ![]() +
+ ![]() =
= ![]() ��
��
C���� ![]() ����
���� ![]() ����ԲC�İ뾶Ϊr=
����ԲC�İ뾶Ϊr= ![]() ��
��
��ƽ�漸��֪ʶ��֪���ڡ�HMC�У���HMC=90�㣻
��HM2=HC2��CM2
= ![]() +
+ ![]() ��
�� ![]()
= ![]() +
+ ![]() +Dx0+Ey0+F��
+Dx0+Ey0+F��
��|HM|= ![]()
��2���⣺��ͼ��ʾ�����A����1��0����ԲP���������ߵ��е�ֱ�ΪM��N��
������֪EB=EM��
��EA+EB=|AM|��
��P������Ϊ��4��y0������ԲP�ķ���Ϊ
��x��4��2+��y��y0��2=9+y02��
��x2+y2��8x��2y0y+7=0��
�ɵڣ����ʵĽ��ۿ�֪
|AM|= ![]() =4��
=4��
��|EA|+|EB|=4��
��������1��������ɵ���RT��HMC��,���ݹ��ɶ����� �ý����
2���ɹ�һ����Բ���������ߵ����ʿɵ�EB=EM���ɵ�Ҫ��Ľ��EA+EB=|AM|�ٸ��ݣ�1���Ľ��ۿ���á�
�����㾫����������Ҫ������ֱ����Բ������λ�ù�ϵ�����֪ʶ�㣬��Ҫ����ֱ����Բ������λ�ù�ϵ��������Ϊ���룻������������Ϊ�ཻ,����ֱ�߽���Բ�ĸ��ߣ�Բ��ֱ����Ψһ������Ϊ���У�����ֱ�߽���Բ�����ߣ����Ψһ�Ĺ���������е������ȷ�����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�