题目内容
2.已知数列{an}的前n项和为Sn,a1=1,an+1=2Sn+1(n∈N*).(1)求数列{an}的通项公式;
(2)求数列{$\frac{2n+1}{{a}_{n}}$}的前n项和Tn.
分析 (1)通过an+1=2Sn+1与an=2Sn-1+1(n≥2)作差、整理可知数列{an}是首项为1、公比为3的等比数列,进而计算可得结论;
(2)通过an=3n-1可知$\frac{2n+1}{{a}_{n}}$=$\frac{2n+1}{{3}^{n-1}}$,利用错位相减法计算即得结论.
解答 解:(1)∵an+1=2Sn+1(n∈N*),
∴an=2Sn-1+1(n≥2),
两式相减得:an+1=3an(n≥2),
由an+1=2Sn+1得:a2=2a1+1=3,
∴a2=3a1满足上式,
∴数列{an}是首项为1、公比为3的等比数列,
∴an=3n-1;
(2)∵an=3n-1,
∴$\frac{2n+1}{{a}_{n}}$=$\frac{2n+1}{{3}^{n-1}}$,
∴Tn=$\frac{3}{{3}^{0}}$+$\frac{5}{3}$+…+$\frac{2n-1}{{3}^{n-2}}$+$\frac{2n+1}{{3}^{n-1}}$,
∴$\frac{1}{3}$Tn=$\frac{3}{3}$+$\frac{5}{{3}^{2}}$+…+$\frac{2n-1}{{3}^{n-1}}$+$\frac{2n+1}{{3}^{n}}$,
两式相减得:$\frac{2}{3}$Tn=3+2($\frac{1}{3}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{3}^{n-1}}$)-$\frac{2n+1}{{3}^{n}}$=4-$\frac{2n+4}{{3}^{n}}$,
∴Tn=6-$\frac{n+2}{{3}^{n-1}}$.
点评 本题考查数列的通项及前n项和,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
17.已知函数f(x)=xcosx+3(-1≤x≤1),设函数f(x)的最大值是M,最小值是N,则( )
| A. | M+N=8 | B. | M+N=6 | C. | M-N=8 | D. | M-N=6 |
14.设变量x,y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{y≥3x-6}\\{x+y≥2}\end{array}\right.$,则目标函数z=2x+y的最小值为( )
| A. | 9 | B. | 4 | C. | 3 | D. | 2 |
12.已知集合M={x|x2+3x=4},N={0,1,2},则M∩N=( )
| A. | ∅ | B. | {1} | C. | {0} | D. | {2} |
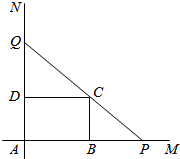 如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ过点C,其中AB=30米,AD=20米.记三角形花园APQ的面积为S.
如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ过点C,其中AB=30米,AD=20米.记三角形花园APQ的面积为S.