Question

已知F₁、F₂是椭圆的两个焦点，P是椭圆上一点，∠F₁PF₂=90°，则椭圆离心率的取值范围是

[

2

2

，1)

．

Answer 1

分析：根据题意，点P即在已知椭圆上，又在以F₁F₂为直径的圆上．因此以F₁F₂为直径的圆与椭圆有公式点，所以该圆的半径c大于或等于短半轴b的长度，由此建立关于a、c的不等式，即可求得椭圆离心率的取值范围．

解答：解∵P点满足∠F₁PF₂=90°，
∴点P在以F₁F₂为直径的圆上
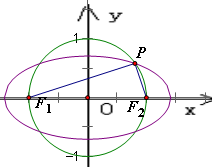
又∵P是椭圆上一点，
∴以F₁F₂为直径的圆与椭圆有公共点，
∵F₁、F₂是椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)的焦点
∴以F₁F₂为直径的圆的半径r满足：r=c≥b，
两边平方，得c²≥b²
即c²≥a²-c²⇒2c²≥a²
两边都除以ea²，得2e²≥1，
∴e≥

2

2

，结合0＜e＜1，
∴

2

2

≤e＜1，即椭圆离心率的取值范围是[

2

2

，1）．
故答案为：[

2

2

，1）．

点评：本题在已知椭圆上一点对两个焦点张角等于90度的情况下，求椭圆的离心率，着重考查了椭圆的基本概念和解不等式的基本知识，属于中档题．