��Ŀ����
ijУѧ����������ѧ�о�С���ڶ�ѧ���Ͽ�ע������������ĵ����о��У�������ע����ָ��P������ʱ��t֮��Ĺ�ϵ������ͼ��ʾ�����ߣ���t�ʣ�0��14]ʱ�������Ƕ��κ���ͼ���һ���֣���t��[14��40]ʱ�������Ǻ���y=log����x-5��+83��a��0��a��1��ͼ���һ���֣�����ר���о�����ע����ָ��P���ڵ���80ʱ����Ч����ѣ�
��1������P=f��t���ĺ�����ϵʽ��
��2����ʦ��ʲôʱ���ڰ��ź���������ʹ��ѧ������Ч����ѣ�
��˵�����ɣ�
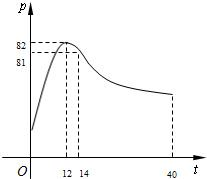
��1������P=f��t���ĺ�����ϵʽ��
��2����ʦ��ʲôʱ���ڰ��ź���������ʹ��ѧ������Ч����ѣ�
��˵�����ɣ�

��1��t�ʣ�0��14]ʱ����p=f��t��=c��t-12��2+82��c��0����
����14��81�������c=-
t�ʣ�0��14]ʱ��p=f��t��=-
��t-12��2+82��4�֣�
t�ʣ�14��40]ʱ������14��81������y=loga��x-5��+83����a=
��6�֣�
��p=f(t)=
����7�֣�
��2��t�ʣ�0��14]ʱ��-
��t-12��2+82��80
���12-2
��t��12+2
��
��t��[12-2
��14]��11�֣�
t��[14��40]ʱ��log
��t-5��+83��80���5��t��32��
��t��[14��32]����t��[12-2
��32]����15�֣�
����ʦ��t��[12-2
��32]ʱ���ڰ��ź���������ʹ��ѧ������Ч����ѣ���16�֣�
����14��81�������c=-
| 1 |
| 4 |
t�ʣ�0��14]ʱ��p=f��t��=-
| 1 |
| 4 |
t�ʣ�14��40]ʱ������14��81������y=loga��x-5��+83����a=
| 1 |
| 3 |
��p=f(t)=
|
��2��t�ʣ�0��14]ʱ��-
| 1 |
| 4 |
���12-2
| 2 |
| 2 |
��t��[12-2
| 2 |
t��[14��40]ʱ��log
| 1 |
| 3 |
��t��[14��32]����t��[12-2
| 2 |
����ʦ��t��[12-2
| 2 |

��ϰ��ϵ�д�
�����Ŀ
 ___________.
___________.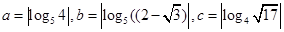 ,��( )
,��( )


