题目内容
已知函数f(x)=a•2x+b•3x,其中常数a,b满足a•b≠0
(1)若a•b>0,判断函数f(x)的单调性;
(2)若a•b<0,求f(x+1)>f(x)时的x的取值范围.
(1)若a•b>0,判断函数f(x)的单调性;
(2)若a•b<0,求f(x+1)>f(x)时的x的取值范围.
(1)①若a>0,b>0,则y=a•2x与y=b•3x均为增函数,所以f(x)=a•2x+b•3x在R上为增函数;
②若a<0,b<0,则y=a•2x与y=b•3x均为减函数,所以f(x)=a•2x+b•3x在R上为减函数.
(2)①若a>0,b<0,
由f(x+1)>f(x)得a•2x+1+b•3x+1>a•2x+b•3x,
化简得a•2x>-2b•3x,即(
)x>
,
解得x<log
;
②若a<0,b>0,
由f(x+1)>f(x)可得(
)x<
,
解得x>log
.
②若a<0,b<0,则y=a•2x与y=b•3x均为减函数,所以f(x)=a•2x+b•3x在R上为减函数.
(2)①若a>0,b<0,
由f(x+1)>f(x)得a•2x+1+b•3x+1>a•2x+b•3x,
化简得a•2x>-2b•3x,即(
| 2 |
| 3 |
| -2b |
| a |
解得x<log
| 2 |
| 3 |
| -2b |
| a |
②若a<0,b>0,
由f(x+1)>f(x)可得(
| 2 |
| 3 |
| -2b |
| a |
解得x>log
| 2 |
| 3 |
| -2b |
| a |

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
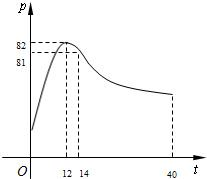
 为常数,其中
为常数,其中 的图象如右图,则下列结论成立的是( )
的图象如右图,则下列结论成立的是( )




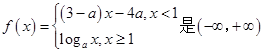 上的增函数,那么
上的增函数,那么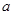 的取值范围是
的取值范围是