题目内容
【题目】观察下列算式:13=1,23=3+5,33=7+9+11,43=13+15+17+19,…若某数n3按上述规律展开后,发现右边含有“2017”这个数,则:n= .
【答案】45
【解析】解:由题意可得第n个式子的左边是n3 , 右边是n个连续奇数的和, 设第n个式子的第一个数为an , 则有a2﹣a1=3﹣1=2,
a3﹣a2=7﹣3=4,…an﹣an﹣1=2(n﹣1),
以上(n﹣1)个式子相加可得an﹣a1= ![]() ,
,
故an=n2﹣n+1,可得a45=1981,a46=2071,
故可知2017在第45个式子,
所以答案是:45
【考点精析】通过灵活运用归纳推理,掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理即可以解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
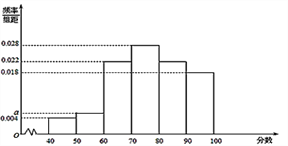
【题目】宿州某中学N名教师参加“低碳节能你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示. 
下表是年龄的频数分布表:
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 25 | m | p | 75 | 25 |
(1)求正整数m,p,N的值;
(2)用分层抽样的方法,从第1、3、5组抽取6人,则第1、3、5组各抽取多少人?
(3)在(2)的条件下,从这6人中随机抽取2人参加学校之间的宣传交流活动,求恰有1人在第3组的概率.