题目内容
【题目】现有一块大型的广告宣传版面,其形状是右图所示的直角梯形![]() .某厂家因产品宣传的需要,拟投资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形
.某厂家因产品宣传的需要,拟投资规划出一块区域(图中阴影部分)为产品做广告,形状为直角梯形![]() (点
(点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() 在线段
在线段![]() 上).已知
上).已知![]() ,
, ![]() ,其中曲线段
,其中曲线段![]() 是以
是以![]() 为顶点,
为顶点, ![]() 为对称轴的抛物线的一部分.
为对称轴的抛物线的一部分.

(1)建立适当的平面直角坐标系,分别求出曲线段![]() 与线段
与线段![]() 的方程;
的方程;
(2)求该厂家广告区域![]() 的最大面积.
的最大面积.
【答案】(1)直角坐标系见解析; 曲线段![]() 的方程为:
的方程为: ![]() ;
;
线段![]() 的方程为:
的方程为: ![]() .
.
(2) ![]() .
.
【解析】试题分析:(1)以AB为x轴,DA为y轴建立平面直角坐标系,则A(0,0),B(6,0),C(6,-12),D(0,-6).设曲线AC的方程x2=-2py,(p>0,0≤x≤6).代入C坐标即可求得p,即可求出曲线段![]() 的方程,由DC两点坐标即可求出线段
的方程,由DC两点坐标即可求出线段![]() 的方程;
的方程;
(2)设出F点横坐标a,将厂家广告区域![]() 的面积表示为a的函数,求出函数的最大值即可.
的面积表示为a的函数,求出函数的最大值即可.
试题解析:(1)以直线![]() 为
为![]() 轴,直线
轴,直线![]() 为
为![]() 轴建立平面直角坐标系(如图所示).
轴建立平面直角坐标系(如图所示).
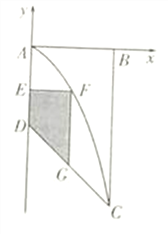
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
曲线段![]() 的方程为:
的方程为: ![]() ;
;
线段![]() 的方程为:
的方程为: ![]() ;
;
(2)设点![]() ,则需
,则需![]() ,即
,即![]() ,
,
则![]() ,
, ![]() ,
, ![]() .
.
∴![]() ,
, ![]() ,
, ![]() ,
,
则厂家广告区域![]() 的面积
的面积
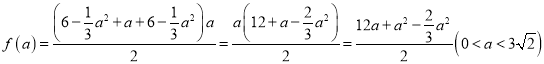 ,
,
∴![]() ,
,
令![]() ,得
,得![]() ,
, ![]() .
.
∴![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
∴![]() .
.
∴厂家广告区域![]() 的面积最大值是
的面积最大值是![]() .
.
点睛:本题利用已知函数模型解决实际问题,关键是合理建系设出点坐标即可表示出面积的表达式,利用导数研究单调性即可求出最值.

【题目】大家知道,莫言是中国首位获得诺贝尔奖的文学家,国人欢欣鼓舞.某高校文学社从男女生中各抽取50名同学调查对莫言作品的了解程度,结果如下:
阅读过莫言的 | 0~25 | 26~50 | 51~75 | 76~100 | 101~130 |
男生 | 3 | 6 | 11 | 18 | 12 |
女生 | 4 | 8 | 13 | 15 | 10 |
(Ⅰ)试估计该校学生阅读莫言作品超过50篇的概率;
(Ⅱ)对莫言作品阅读超过75篇的则称为“对莫言作品非常了解”,否则为“一般了解”.根据题意完成下表,并判断能否有75%的把握认为对莫言作品的非常了解与性别有关?
非常了解 | 一般了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
附:K2=![]()
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
