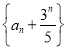题目内容
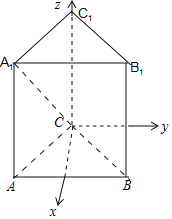
【题目】如图,正三棱柱
底面三角形的周长为6,侧棱长
长为3.
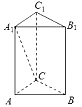
(1)求正三棱柱的体积；
(2)求异面直线
与AB所成角的大小.
【答案】（1）
（2）
【解析】
（1）由已知求得三棱柱底面边长，得到底面积，再由棱柱体积公式求解；
（2）以C为坐标原点，以过C且垂直于AB的直线为x轴，以过C且平行于AB的直线为y轴，以CC1所在直线为z轴建立空间直角坐标系，利用空间向量求解．
解：（1）∵正三棱柱ABC﹣A1B1C1底面三角形的周长为6，∴边长为2，
则AB边上的高为
，
∴
，
又侧棱长AA1长为3，
则正三棱柱ABC﹣A1B1C1的体积V＝
；
（2）以C为坐标原点，以过C且垂直于AB的直线为x轴，以过C且平行于AB的直线为y轴，
以CC1所在直线为z轴建立空间直角坐标系，
则C（0，0，0），A
，B
，A1
，
，
∴cos
＝
＝
．
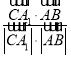∴异面直线A1C与AB所成角的大小为．
练习册系列答案
相关题目
