题目内容
如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是________.
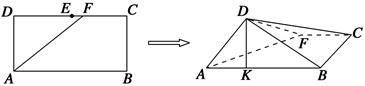

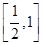
如图,过D作DG⊥AF,垂足为G,连接GK,∵平面ABD⊥平面ABC,DK⊥AB,∴DK⊥平面ABC,∴DK⊥AF.又DG⊥AF,∴AF⊥平面DKG,∴AF⊥GK.
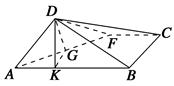
容易得到,当F运动到E点时,K为AB的中点,t=AK=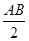 =1;当F运动到C点时,在Rt△ADF中,易得AF=
=1;当F运动到C点时,在Rt△ADF中,易得AF=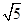 ,且AG=
,且AG=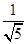 ,GF=
,GF=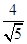 ,又易知Rt△AGK∽Rt△ABF,则
,又易知Rt△AGK∽Rt△ABF,则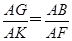 ,又AB=2,AK=t,则t=
,又AB=2,AK=t,则t=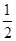 .∴t的取值范围是
.∴t的取值范围是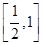 .
.

容易得到,当F运动到E点时,K为AB的中点,t=AK=
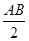 =1;当F运动到C点时,在Rt△ADF中,易得AF=
=1;当F运动到C点时,在Rt△ADF中,易得AF=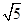 ,且AG=
,且AG=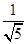 ,GF=
,GF=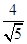 ,又易知Rt△AGK∽Rt△ABF,则
,又易知Rt△AGK∽Rt△ABF,则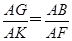 ,又AB=2,AK=t,则t=
,又AB=2,AK=t,则t=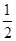 .∴t的取值范围是
.∴t的取值范围是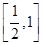 .
.
练习册系列答案
相关题目
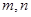 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,下列四个命题中假命题的是( )
是三个不同的平面,下列四个命题中假命题的是( ) 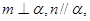 则
则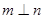
 则
则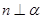
 则
则
 ,则
,则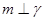
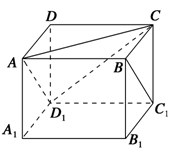
 //平面
//平面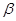 ,
,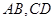 是夹在
是夹在 间的线段,若
间的线段,若 //
//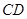 ,则
,则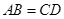 ;
; 是异面直线,
是异面直线,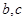 是异面直线,则
是异面直线,则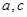 一定是异面直线;
一定是异面直线;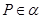 ,
, //
//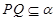 ;
;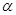 、
、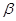 表示不同的平面,
表示不同的平面,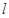 、
、 、
、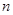 表示不同直线,则以下命题中正确的有 ( )
表示不同直线,则以下命题中正确的有 ( )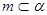 ,
,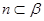 ,则
,则